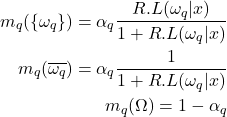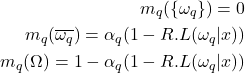Comment décider en présence d’imprécision ?
S. Sochacki, PhD in Computer Science
A2D, ZA Les Minimes, 1 rue de la Trinquette, 17000 La Rochelle, FRANCE
1 Introduction
Imprécision/incertitude/conflit
AI Act, explicabilité
Comment décider en informatique ? Sur quoi se base un système automatique pour prendre une décision ? Bien souvent, ce genre de système s’appuie sur un principe de règles de décision (souvent probabilistes), ou encore sur une approche pignistique (un niveau entièrement dédié à la prise de décision et clairement séparé de la modélisation des données).
Bien qu’une très grande partie des applications traitement d’images grand public soit tournée vers l’amélioration, la restauration ou le traitement des photographies ; dans le cadre industriel, les applications visées portent sur la prise de décision à partir des images. Si les classes d’information utilisées à cette fin sont connues (texture, forme, couleur), elles ne présentent pas toutes le même intérêt dans l’aide à la prise de décision. Dés lors, différentes formes d’apprentissage ont été développées pour identifier le meilleur assemblage possible des informations. Des dizaines de solutions existent pour répondre à cette question, certaines même combinent plusieurs de ces approches pour optimiser au maximum la prise de décision.
Néanmoins, si toutes les classes d’information, et de façon plus fine tous les opérateurs d’extraction d’information (moments de Zernike, attributs D’Haralick, pour n’en citer que deux), ne présentent pas le même intérêt pour la prise de décision, les informations extraites sont quant à elles jugées toutes de même qualité. Or, le traitement d’images provient pour partie du traitement du signal et par là même, du monde de la physique et plus particulièrement de la métrologie. Nous sommes donc bien loin d’un monde binaire, où l’information est vraie ou fausse mais certaine quant à son affectation. En métrologie, la mesure n’existe que liée à un critère de précision ou tolérance. Ce critère quantifie la plage de valeurs au sein de laquelle la mesure se situe avec une bonne certitude. Ce point de vue typique de la métrologie conduite avec des appareils à aiguille est bien souvent oublié lors du passage au numérique. Pourtant, tout scientifique reste sceptique lors de l’annonce d’un résultat avec plus de 3 chiffres derrière la virgule (lorsque cette précision n’a pas été justifiée au préalable).
A2D s’applique à développer des applications utilisant des algorithmes de prise de décision pour répondre à ces nouveaux besoins, en respectant les contraintes liées à l’IA de confiance (AI Act ![]() , ISO/IEC 42001
, ISO/IEC 42001 ![]() ) et à la sobriété énergétique. En pratique, nous concevons des applications de traitement et d’analyse de données permettant de comprendre les scènes d’extérieur, numérisées en vue d’y détecter des zones d’intérêt précises, dépendant des usages Métier.
) et à la sobriété énergétique. En pratique, nous concevons des applications de traitement et d’analyse de données permettant de comprendre les scènes d’extérieur, numérisées en vue d’y détecter des zones d’intérêt précises, dépendant des usages Métier.
Nous nous applicons également à fournir, à tout moment au cours du traitement de l’information, une explicapibilité quant aux résultats obtenus et aux choix proposés par la machine.
2 Approche probabiliste
Puisque nous cherchons à proposer une nouvelle extension aux outils de prise de décision, il nous apparaissait important de rester dans le cadre des outils à fond mathématique, par opposition aux outils construits sur des bases de règles. Comme les probabilités sont au cœur de ces approches, nous avons choisi de démarrer cette étude à partir de ce formalisme.
Classiquement, nous appelons probabilité, l’évaluation du caractère probable d’un évènement. Elle est représentée par un nombre réel compris entre 0 et 1, indiquant le degré de risque (ou de chance) que l’évènement se produise. Dans l’exemple typique du lancer de pièce de monnaie, l’évènement « coté pile » présente une probabilité de ![]() , ce qui signifie qu’après avoir lancé la pièce un très grand nombre de fois, la fréquence d’apparition de « coté pile » sera de
, ce qui signifie qu’après avoir lancé la pièce un très grand nombre de fois, la fréquence d’apparition de « coté pile » sera de ![]() .
.
En probabilité, un évènement peut être à peu près tout ce que l’on imagine, pouvant se produire ou non. Cela peut être le fait qu’il fasse beau demain ou le fait d’obtenir le chiffre 6 en lançant un dé. La seule contrainte est de pouvoir vérifier l’évènement ; il est tout à fait possible de vérifier s’il fera beau demain (évènement que l’on mesure de façon personnelle, le lendemain, en fonction de ses goûts en matière d’ensoleillement, de température etc.), ou si on arrive à obtenir un chiffre 6 avec un dé.
Nous dirons qu’un évènement ayant une probabilité de 0 est impossible, tandis qu’un évènement ayant une probabilité de 1 est certain.
Notons que la probabilité est un outil de prédiction d’évènements du monde réel, et non un outil d’explication de celui-ci. Il s’agit d’étudier des ensembles en les mesurant.
2.1 Définitions
Une expérience est dite aléatoire quand son résultat n’est pas prévisible. Définissons alors ![]() , une expérience aléatoire ayant pour résultat
, une expérience aléatoire ayant pour résultat ![]() un élément de
un élément de ![]() , l’ensemble de tous les résultats possibles, appelé univers des possibles ou référentiel.
, l’ensemble de tous les résultats possibles, appelé univers des possibles ou référentiel.
Soit ![]() l’ensemble des parties de
l’ensemble des parties de ![]() . Un événement est alors une proposition logique liée à une expérience, relative au résultat de celle-ci.
. Un événement est alors une proposition logique liée à une expérience, relative au résultat de celle-ci.
Notons ![]() l’ensemble des événements et sous-ensemble de
l’ensemble des événements et sous-ensemble de ![]() . Pour tout
. Pour tout ![]() et
et ![]() :
:
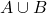 désigne la réalisation de
désigne la réalisation de 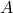 ou
ou 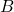
 désigne la réalisation de
désigne la réalisation de 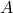 et
et 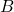
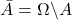 désigne le contraire de
désigne le contraire de 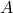
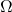 est l’événement certain
est l’événement certain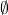 est l’événement impossible
est l’événement impossible
Quand le référentiel ![]() est fini,
est fini, ![]() désigne toutes les parties de
désigne toutes les parties de ![]() , noté habituellement
, noté habituellement ![]() . Quand le référentiel est
. Quand le référentiel est ![]() (ou un intervalle de
(ou un intervalle de ![]() ) la notion de tribu permet de définir
) la notion de tribu permet de définir ![]() :
:
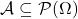
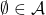
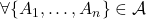 ,
, 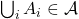 et
et 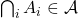
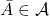

Une mesure de probabilité sur un espace mesurable ![]() est une fonction de
est une fonction de ![]() dans
dans ![]() telle que :
telle que :
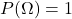
- Pour tous les éléments
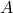 et
et 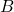 incompatibles (i.e.
incompatibles (i.e. 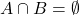 ),
), 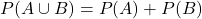
Le nombre ![]() quantifie dans quelle mesure l’événement
quantifie dans quelle mesure l’événement ![]() est probable.
est probable.
Dans le cas du lancer de dé, nous pouvons affirmer que ![]() représente l’ensemble des 6 faces du dé. Ainsi, la probabilité d’obtenir un chiffre compris entre 1 et 6 est certaine, donc égale à 1. Nous écrirons donc
représente l’ensemble des 6 faces du dé. Ainsi, la probabilité d’obtenir un chiffre compris entre 1 et 6 est certaine, donc égale à 1. Nous écrirons donc ![]() .
.
De la même façon, la probabilité d’obtenir 1 (ou 2, ou 3, ou 4 etc.) est de 1/6. Donc, ![]() .
.
En lien avec ![]() , dans le cas où
, dans le cas où ![]() est fini, une distribution de probabilité est définie comme une fonction
est fini, une distribution de probabilité est définie comme une fonction ![]() de
de ![]() dans
dans ![]() , telle que :
, telle que :
(2.1.1) ![]()
avec la condition de normalisation :
(2.1.2) ![]()
Notons que ![]() .
.
2.2 Règle de Bayes
L’introduction d’un modèle statistique conduit à une théorie de la décision directement applicable, en principe, au problème de la classification. Cette application repose essentiellement sur la règle de Bayes qui permet d’évaluer des probabilités a posteriori (c’est à dire après l’observation effective de certaines grandeurs) connaissant les distributions de probabilité conditionnelles a priori (c’est-à-dire indépendantes de toute contrainte sur les variables observées). Les probabilités nécessaires à la prise de décision selon la règle de Bayes sont apportées par un (ou plusieurs) classifieur statistique qui indique la probabilité d’appartenance d’un individu donné à chaque classe du problème.
En théorie des probabilités, le théorème de Bayes énonce des probabilités conditionnelles : étant donné deux évènements ![]() et
et ![]() , le théorème de Bayes permet de déterminer la probabilité de
, le théorème de Bayes permet de déterminer la probabilité de ![]() sachant
sachant ![]() , si l’on connaît les probabilités : de
, si l’on connaît les probabilités : de ![]() , de
, de ![]() et de
et de ![]() sachant A. Pour aboutir au théorème de Bayes, il faut partir d’une des définitions de la probabilité conditionnelle :
sachant A. Pour aboutir au théorème de Bayes, il faut partir d’une des définitions de la probabilité conditionnelle : ![]() , en notant
, en notant ![]() la probabilité que
la probabilité que ![]() et
et ![]() aient lieu tous les deux. En divisant de part et d’autre par
aient lieu tous les deux. En divisant de part et d’autre par ![]() , on obtient
, on obtient ![]() soit le théorème de Bayes. Chaque terme du théorème de Bayes a une dénomination usuelle. Le terme
soit le théorème de Bayes. Chaque terme du théorème de Bayes a une dénomination usuelle. Le terme ![]() est la probabilité a priori de A. Elle est « antérieure » au sens qu’elle précède toute information sur
est la probabilité a priori de A. Elle est « antérieure » au sens qu’elle précède toute information sur ![]() .
. ![]() est aussi appelée la probabilité marginale de
est aussi appelée la probabilité marginale de ![]() . Le terme
. Le terme ![]() est appelée la probabilité a posteriori de
est appelée la probabilité a posteriori de ![]() sachant
sachant ![]() (ou encore de
(ou encore de ![]() sous condition
sous condition ![]() ) . Elle est « postérieure », au sens qu’elle dépend directement de
) . Elle est « postérieure », au sens qu’elle dépend directement de ![]() . Le terme
. Le terme ![]() , pour un
, pour un ![]() connu, est appelé la fonction de vraisemblance de
connu, est appelé la fonction de vraisemblance de ![]() . De même, le terme
. De même, le terme ![]() est appelé la probabilité marginale ou a priori de
est appelé la probabilité marginale ou a priori de ![]() .
.
Mais, comme énoncé précédemment, les valeurs des probabilités utilisées par la règle de Bayes sont apportées par des classifieurs statistiques, voire tout simplement par estimation des lois de probabilités de chacune des classes.
2.3 Prise de décision statistique
Depuis l’hypothèse sur les lois de probabilités des classes du problème (et ses tests de validation) jusqu’à la mesure de la distance au centre de chaque classe en passant par différentes formes d’estimation de modèle, il existe dans le domaine des statistiques un très grand nombre de méthodes et notre propos n’est pas d’en faire une étude exhaustive mais de comparer les théories (statistiques, théorie de la décision…) sur le principe.
Sachons seulement qu’il existe notamment deux types d’approches statistiques : les classifieurs linéaires et les classifieurs quadratiques. Les premiers sont appelés ainsi car leur approche consiste à partitionner l’espace des attributs de façon simple, à partir de droites, chaque droite symbolisant la frontière entre deux classes, comme l’illustre la frontière en vert sur la figure 2.3.1. La seconde approche est plus complexe car elle tente d’estimer la forme des frontières entre les régions, c’est ainsi que l’on obtient la séparation circulaire entre les classes.
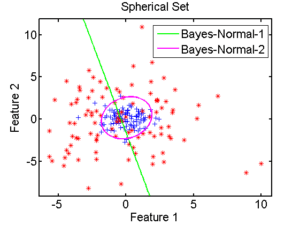
2.3.1 Classifieur Bayesien [93][4][14]
La théorie de la décision de Bayes est une approche statistique du problème. Elle est basée sur les hypothèses suivantes :
- Le problème de la décision est exprimé en terme de probabilités
- La valeur des probabilités a priori du tirage d’une classe est connue
Soit ![]() , une variable aléatoire représentant l’état de l’individu (
, une variable aléatoire représentant l’état de l’individu (![]() si l’individu appartient à la classe
si l’individu appartient à la classe ![]() ).
).
Soit ![]() ensemble des
ensemble des ![]() états possibles ou classes d’un problème.
états possibles ou classes d’un problème.
L’ensemble des probabilités a priori ![]() est calculé à partir des d’observations réalisées sur le système étudié. En l’absence d’autres informations, il ne reste d’autre choix que d’écrire
est calculé à partir des d’observations réalisées sur le système étudié. En l’absence d’autres informations, il ne reste d’autre choix que d’écrire ![]() individu
individu ![]() . Mais s’il est possible d’obtenir d’autres informations (mesures), alors
. Mais s’il est possible d’obtenir d’autres informations (mesures), alors ![]() , densité de probabilité de
, densité de probabilité de ![]() sachant que l’individu est
sachant que l’individu est ![]() , ou densité de probabilité conditionnelle à son appartenance à
, ou densité de probabilité conditionnelle à son appartenance à ![]() , est calculable.
, est calculable.
![]() est donc la probabilité d’apparition a priori de la classe
est donc la probabilité d’apparition a priori de la classe ![]() et
et ![]() est la probabilité que la forme caractérisée par le vecteur
est la probabilité que la forme caractérisée par le vecteur ![]() appartienne à
appartienne à ![]() .
.
Dans ce cas, nous disposons de ![]() , le vecteur aléatoire (mesures ou situation) sur
, le vecteur aléatoire (mesures ou situation) sur ![]() . Le problème devient alors : soit un individu et sa mesure
. Le problème devient alors : soit un individu et sa mesure ![]() . Comment décider à quelle catégorie (
. Comment décider à quelle catégorie (![]() ) affecter cet individu ?
) affecter cet individu ?
La règle de Bayes donne la réponse :
(2.3.1.1) ![]()
avec
(2.3.1.2) 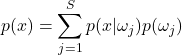
où ![]() est le nombre de classes différentes et
est le nombre de classes différentes et ![]() la distribution de probabilité pour l’ensemble des individus (densité de probabilité du vecteur
la distribution de probabilité pour l’ensemble des individus (densité de probabilité du vecteur ![]() ), dans laquelle les échantillons de chaque classe
), dans laquelle les échantillons de chaque classe ![]() apparaissent proportionnellement aux probabilités a priori
apparaissent proportionnellement aux probabilités a priori ![]() ; c’est le facteur de normalisation.
; c’est le facteur de normalisation.
La règle de décision est alors la suivante :
Il reste à présent à exprimer les densités de probabilité conditionnelle. Pour cela, rappelons l’inégalité de Bienaymé-Tchebicheff :
Soient ![]() des variables aléatoires indépendantes, toutes d’espérance
des variables aléatoires indépendantes, toutes d’espérance ![]() et de variance
et de variance ![]() . Soit
. Soit ![]() alors pour tout
alors pour tout ![]() :
:
(2.3.1.3) ![]()
La probabilité qu’une variable aléatoire s’écarte de plus de d de sa valeur moyenne est d’autant plus faible que sa variance est petite et que d est grand. En particulier (Loi des grands nombres) [7] :
(2.3.1.4) ![]()
Si ![]() , il est admis, en appliquant le théorème central-limite (qui affirme intuitivement que toute somme de variables aléatoires indépendantes et identiquement distribuées tend vers une variable aléatoire gaussienne), que
, il est admis, en appliquant le théorème central-limite (qui affirme intuitivement que toute somme de variables aléatoires indépendantes et identiquement distribuées tend vers une variable aléatoire gaussienne), que ![]() suit pratiquement une loi Normale. Rappelons que la densité d’une loi Normale est de la forme (sur une dimension) :
suit pratiquement une loi Normale. Rappelons que la densité d’une loi Normale est de la forme (sur une dimension) :
(2.3.1.5) ![]()
Enfin, nous savons que l’espérance mathématique d’une variable aléatoire peut être estimée ponctuellement par :
(2.3.1.6) ![]()
Donc, pour notre mesure ![]() , les échantillons sont supposés suivre une loi Normale
, les échantillons sont supposés suivre une loi Normale ![]() dont la densité de probabilité sera exprimée sous forme matricielle :
dont la densité de probabilité sera exprimée sous forme matricielle :
(2.3.1.7) ![]()
avec ![]() moyenne d’une classe,
moyenne d’une classe, ![]() matrice de covariance de la classe
matrice de covariance de la classe ![]() et
et ![]() déterminant de la matrice de covariance de la classe
déterminant de la matrice de covariance de la classe ![]() .
.
La probabilité conditionnelle est donc exprimée par l’équation suivante :
(2.3.1.8) ![]()
L’opération de classification consistera à calculer pour chaque mesure ![]() sa probabilité d’appartenance à toutes les classes, et de l’affecter à la classe qui vérifie la probabilité a posteriori maximum.
sa probabilité d’appartenance à toutes les classes, et de l’affecter à la classe qui vérifie la probabilité a posteriori maximum.
2.3.2 Les k-plus proches voisins (KPPV ou KNN)
Cette approche consiste à prendre dans l’espace des attributs un nombre donné (![]() ) d’individus connus, individus choisis dans le voisinage de l’individu dont on cherche à estimer la classe d’appartenance. C’est à la connaissance des classes représentées dans ce voisinage que se fait l’étiquetage de l’individu inconnu.
) d’individus connus, individus choisis dans le voisinage de l’individu dont on cherche à estimer la classe d’appartenance. C’est à la connaissance des classes représentées dans ce voisinage que se fait l’étiquetage de l’individu inconnu.
La règle des k-plus proches voisins a été formalisée par Fix et Hodges [5] dans les années 50. Cette règle consiste à baser le choix du voisinage ![]() sur le nombre d’observations qu’il contient fixé à
sur le nombre d’observations qu’il contient fixé à ![]() parmi le nombre total d’observations
parmi le nombre total d’observations ![]() . Autrement dit, il s’agit de sélectionner dans l’ensemble des observations, un sous-ensemble de
. Autrement dit, il s’agit de sélectionner dans l’ensemble des observations, un sous-ensemble de ![]() individus. C’est le volume
individus. C’est le volume ![]() de
de ![]() qui est variable. L’estimateur de la densité de probabilité s’exprime alors de la façon suivante :
qui est variable. L’estimateur de la densité de probabilité s’exprime alors de la façon suivante :
(2.3.2.1) ![]()
Cette estimation n’est valable que dans les conditions suivantes :
![]()
La première hypothèse correspond à un espace complètement occupé par les observations : quand le nombre d’observations est infini, ces observations occupent l’espace de façon uniforme. La seconde hypothèse considère que, pour un nombre infini d’observations, tout sous-ensemble de cardinal ![]() est occupé par un nombre infini d’éléments répartis uniformément.
est occupé par un nombre infini d’éléments répartis uniformément.
Dans le cadre de la classification supervisée, la loi de probabilité conditionnelle peut être approximée par :
(2.3.2.2) ![]()
où ![]() est le nombre d’observations contenues dans le volume
est le nombre d’observations contenues dans le volume ![]() appartenant à la classe d’étiquette
appartenant à la classe d’étiquette ![]() et
et ![]() le nombre total d’observations appartenant à la classe
le nombre total d’observations appartenant à la classe ![]() . La loi a posteriori d’observation d’une étiquette conditionnellement à une observation s’obtient avec la règle de Bayes :
. La loi a posteriori d’observation d’une étiquette conditionnellement à une observation s’obtient avec la règle de Bayes :
(2.3.2.3) 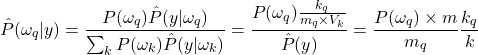
Le choix de ![]() est lié à la base d’apprentissage. Prendre
est lié à la base d’apprentissage. Prendre ![]() élevé permet d’exploiter au mieux les propriétés locales mais nécessite un grand nombre d’échantillons pour contraindre le volume du voisinage à rester petit. Bien souvent,
élevé permet d’exploiter au mieux les propriétés locales mais nécessite un grand nombre d’échantillons pour contraindre le volume du voisinage à rester petit. Bien souvent, ![]() est choisi comme la racine carrée du nombre moyen d’élément par classe soit
est choisi comme la racine carrée du nombre moyen d’élément par classe soit ![]() [2].
[2].
2.4 Synthèse
Mais comment alors choisir autre chose que ce qui est statistiquement le plus probable ?
Se pose alors le problème de la mesure d’une précision d’une décision accompagnée de la production d’une mesure de la précision, même si le problème peut être cette mesure.
3 Théorie de l’évidence
Le modèle des croyances transférables MCT (TBM : transferable belief model) est un cadre formel générique développé par Philippe Smets [20] pour la représentation et la combinaison des connaissances. Le TBM est basé sur la définition de fonctions de croyance fournies par des sources d’information pouvant être complémentaires, redondantes et éventuellement non-indépendantes. Il propose un ensemble d’opérateurs permettant de combiner ces fonctions. Il est donc naturellement employé dans le cadre de la fusion d’informations pour améliorer l’analyse et l’interprétation de données issues de sources d’informations multiples. Ce cadre correspond naturellement à celui qui nous préoccupe par son aspect de prise de décision grâce à différentes informations issues de différents attributs.
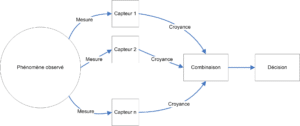
L’un des points fondamentaux qui caractérisent le TBM est la différenciation des niveaux de représentation des connaissances et de décision. Cette différenciation est beaucoup moins prépondérante pour d’autres approches, particulièrement pour le modèle probabiliste pour lequel la décision est souvent le seul objectif visé. Les mécanismes de raisonnement du TBM sont donc regroupés en deux niveaux comme illustré sur la figure 3.1 :
- Le niveau crédal : siège de la représentation des connaissances (partie statique), des combinaisons et du raisonnement sur ces connaissances (partie dynamique)
- Le niveau pignistique indiquant une prise de décision en prenant éventuellement en compte le risque et/ou le gain associés à cette décision.

Dans le cadre de la représentation sous forme de chaîne de traitements, nous nous retrouvons confrontés au problème de l’observation du même événement par plusieurs sources, et de la combinaison de l’information apportée par ces sources (voir figure 3.2), imposant les questions suivantes :
- Comment représenter la connaissance d’une source d’information sous forme de fonctions de croyance et quels avantages peut-on tirer d’une telle représentation?
- Comment combiner plusieurs sources de fonctions de croyance afin de résumer l’information et d’améliorer la prise de décision?
- Comment prendre une décision à partir des fonctions de croyance?
3.1 Présentation
Considérons l’exemple d’une reconnaissance de chiffres manuscrits. Les chiffres possibles pouvant être écrits sont appelés hypothèses et l’ensemble des hypothèses forment le cadre de discernement généralement noté ![]() . Pour notre exemple,
. Pour notre exemple, ![]() où
où ![]() est le symbole représentant le chiffre
est le symbole représentant le chiffre ![]() . Deux hypothèses ne pouvant être vraies simultanément (on ne peut écrire un symbole représentant à la fois plusieurs chiffres), elles sont supposées être exclusives, ce qui se traduit par une intersection nulle entre elles (i.e.
. Deux hypothèses ne pouvant être vraies simultanément (on ne peut écrire un symbole représentant à la fois plusieurs chiffres), elles sont supposées être exclusives, ce qui se traduit par une intersection nulle entre elles (i.e. ![]() ). Supposons maintenant que le document que nous sommes en train d’étudier soit dégradé, ou bien que le chiffre soit très mal écrit, un lecteur donnerait alors un avis pondéré sur ce chiffre, faisant de lui une source d’information. Avec sa connaissance disponible, le lecteur affirme qu’il s’agit soit du chiffre
). Supposons maintenant que le document que nous sommes en train d’étudier soit dégradé, ou bien que le chiffre soit très mal écrit, un lecteur donnerait alors un avis pondéré sur ce chiffre, faisant de lui une source d’information. Avec sa connaissance disponible, le lecteur affirme qu’il s’agit soit du chiffre ![]() , soit
, soit ![]() ou soit
ou soit ![]() . La question est de savoir comment représenter cette information.
. La question est de savoir comment représenter cette information.
Dans le cadre de la théorie des probabilités, la réponse est donnée par le principe d’équiprobabilité, c’est à dire que chaque chiffre se voit attribué la même probabilité (![]() ) de sorte que la somme de toutes les probabilités soit égale à 1. Ainsi, la distribution des probabilités pour ce chiffre est égale à :
) de sorte que la somme de toutes les probabilités soit égale à 1. Ainsi, la distribution des probabilités pour ce chiffre est égale à :
![]()
Cette probabilité n’est affectée qu’à des hypothèses prises seules (appelées également singletons).
En théorie de l’évidence, la notion principale est celle de fonctions de croyance au sein de laquelle la connaissance est modélisée par une distribution de masses de croyance. Dans notre exemple, toute la masse de croyance (une unité entière comme avec les probabilités) est affectée à l’union de toutes les hypothèses, soit la proposition ![]() :
:
![]()
Comme nous pouvons le constater, cette masse ne nous donne aucune information concernant la croyance de chacune des hypothèses (![]() ,
, ![]() et
et ![]() ) qui la compose. Nous pouvons dire alors que la masse de croyance modélise explicitement le doute (ou l’ignorance) sur cet ensemble d’hypothèses. Pour revenir à la théorie des probabilités, la valeur de la probabilité sur une union d’hypothèses découle implicitement de la probabilité sur les singletons, probabilité établie à partir de la somme de toutes les probabilités privée de la partie commune, c’est à dire la probabilité de l’intersection. Soit par exemple :
) qui la compose. Nous pouvons dire alors que la masse de croyance modélise explicitement le doute (ou l’ignorance) sur cet ensemble d’hypothèses. Pour revenir à la théorie des probabilités, la valeur de la probabilité sur une union d’hypothèses découle implicitement de la probabilité sur les singletons, probabilité établie à partir de la somme de toutes les probabilités privée de la partie commune, c’est à dire la probabilité de l’intersection. Soit par exemple :
![]()
Ici, la probabilité sur ![]() représente la partie commune des évènements « Le chiffre est 1 » et « Le chiffre est 7 » que nous devons retirer afin de ne pas compter les évènements deux fois. Dans le cas où les hypothèses sont exclusives (cas que nous retrouverons tout au long de cet article), on obtient :
représente la partie commune des évènements « Le chiffre est 1 » et « Le chiffre est 7 » que nous devons retirer afin de ne pas compter les évènements deux fois. Dans le cas où les hypothèses sont exclusives (cas que nous retrouverons tout au long de cet article), on obtient :
![]()
en prenant en compte le fait que ![]() par définition.
par définition.
Contrairement aux probabilités, une fonction de masse sur une union d’hypothèses n’est pas égale à la somme des masses des hypothèses composant l’union [10], et c’est justement grâce à cette propriété que nous représentons le doute entre des hypothèses. De plus, les fonctions de croyance ont pour avantage d’être génériques, car elles sont la représentation mathématique d’un sur-ensemble de fonctions de probabilités. En effet, une distribution de masses, où seules les hypothèses singletons ont une masse non nulle, est interprétable comme une distribution de probabilités. Klir et Wierman expliquent dans [10] que les fonctions de croyance généralisent mathématiquement les fonctions de possibilités et que chacune de ces fonctions (probabilités, possibilités et croyances) possède des caractéristiques particulières et permettent de modéliser la connaissance différemment.
Voyons à présent le formalisme mathématique des fonctions de croyance, basé sur les modèles de Dempster [6][7], Shafer [15], des croyances transférables [20] et sur le modèle des Hints [9]. Pour ce travail, nous nous sommes restreints au cadre axiomatisé et formalisé du modèle des croyances transférables développé par P. Smets.
3.2 Formalisme
3.2.1 Introduction
Si nous revenons au problème de la gestion de sources multiples d’informations (comme illustré par la figure 3.2), ce que nous cherchons à faire est de déterminer l’état réel ![]() du système étudié en utilisant plusieurs observations issues de plusieurs observateurs. Dans notre cas,
du système étudié en utilisant plusieurs observations issues de plusieurs observateurs. Dans notre cas, ![]() sera la décision à produire et les différents attributs fournissent les observations sur le système.
sera la décision à produire et les différents attributs fournissent les observations sur le système.
Nous supposons que cet état ![]() prend des valeurs discrètes
prend des valeurs discrètes ![]() (les hypothèses) et que l’ensemble des
(les hypothèses) et que l’ensemble des ![]() hypothèses possibles est appelé cadre de discernement (ou \textbf{univers de discours}), noté généralement :
hypothèses possibles est appelé cadre de discernement (ou \textbf{univers de discours}), noté généralement :
(3.2.1.1) 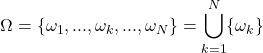
Le nombre total d’hypothèses composant ![]() est appelé cardinal et s’écrit comme
est appelé cardinal et s’écrit comme ![]() . Comme nous l’avons vu précédemment, toutes les hypothèses sont considérées exclusives.
. Comme nous l’avons vu précédemment, toutes les hypothèses sont considérées exclusives.
L’ensemble des observateurs du système (les capteurs de la figure 3.2) fournit un avis pondéré, représenté grâce à une fonction de croyance, à propos de son état réel ![]() . Nous appelons alors ces capteurs, des sources de croyance.
. Nous appelons alors ces capteurs, des sources de croyance.
3.2.2 Fonctions de masse
Notons ![]() l’espace formé de toutes les parties de
l’espace formé de toutes les parties de ![]() , c’est à dire l’espace rassemblant tous les sous-ensembles possibles formés des hypothèses et unions d’hypothèses, soit :
, c’est à dire l’espace rassemblant tous les sous-ensembles possibles formés des hypothèses et unions d’hypothèses, soit :
![]()
Soit ![]() une proposition telle que
une proposition telle que ![]() , par exemple
, par exemple ![]() .
. ![]() représente explicitement le doute entre les hypothèses qui la compose (
représente explicitement le doute entre les hypothèses qui la compose (![]() et
et ![]() ). Comme nous l’avons vu plus haut, les masses de croyances sont non-additives, ce qui est une différence fondamentale avec la théorie des probabilités. Ainsi, la masse de croyance
). Comme nous l’avons vu plus haut, les masses de croyances sont non-additives, ce qui est une différence fondamentale avec la théorie des probabilités. Ainsi, la masse de croyance ![]() allouée à
allouée à ![]() ne donne aucune information à propos des hypothèses et sous ensembles composant
ne donne aucune information à propos des hypothèses et sous ensembles composant ![]() [10].
[10].
Nous pouvons définir une distribution de masses de croyance (BBA : basic belief assignment) comme un ensemble de masses de croyance concernant des propositions quelconques ![]() vérifiant:
vérifiant:
(3.2.2.1) ![]()
Chacun des capteurs observant le système apportera sa propre distribution de masse.
La masse ![]() fournie par un capteur est la part de croyance de ce capteur en la proposition «
fournie par un capteur est la part de croyance de ce capteur en la proposition « ![]() » où
» où ![]() est l’état réel du système observé. Tout élément
est l’état réel du système observé. Tout élément ![]() de masse non nulle (soit
de masse non nulle (soit ![]() ) est appelé élément focal de la distribution de masses de croyance. Ramasso [13] présente dans son mémoire de Thèse un ensemble notable de distributions de masses de croyance.
) est appelé élément focal de la distribution de masses de croyance. Ramasso [13] présente dans son mémoire de Thèse un ensemble notable de distributions de masses de croyance.
Quand l’univers du discours contient la totalité des hypothèses possibles (c’est à dire lorsqu’il est exhaustif), il contient forcément l’hypothèse permettant de décrire le système observé. Dans le cas contraire, le cadre de discernement n’est pas adapté au problème traité.
A partir du moment où ![]() est exhaustif, la masse de l’ensemble vide est nulle (
est exhaustif, la masse de l’ensemble vide est nulle (![]() ), la masse est dite normale, et la problématique entre alors dans le cadre d’un monde fermé comme dans le cas du modèle de Shafer [15].
), la masse est dite normale, et la problématique entre alors dans le cadre d’un monde fermé comme dans le cas du modèle de Shafer [15].
Dans le cas du modèle des croyances transférables, l’univers du discours peut être non exhaustif; la masse de l’ensemble est non nulle (![]() ) et elle est dite sous normale et dans ce cas, la problématique s’inscrit dans le cadre d’un monde ouvert. Ce type de construction permet de redéfinir, par exemple, le cadre de discernement en ajoutant une hypothèse en fonction de la masse de l’ensemble vide, comme une hypothèse de rejet. Les hypothèses de rejet correspondent à des états du genre « je ne sais pas » , permettant en fin de chaîne de rejeter un individu pour lequel le doute est trop grand au lieu de prendre le risque de le classer malgré tout. Pour passer d’un monde ouvert à un monde fermé, il faut redistribuer la masse de l’ensemble vide sur les autres sous-ensembles de l’espace
) et elle est dite sous normale et dans ce cas, la problématique s’inscrit dans le cadre d’un monde ouvert. Ce type de construction permet de redéfinir, par exemple, le cadre de discernement en ajoutant une hypothèse en fonction de la masse de l’ensemble vide, comme une hypothèse de rejet. Les hypothèses de rejet correspondent à des états du genre « je ne sais pas » , permettant en fin de chaîne de rejeter un individu pour lequel le doute est trop grand au lieu de prendre le risque de le classer malgré tout. Pour passer d’un monde ouvert à un monde fermé, il faut redistribuer la masse de l’ensemble vide sur les autres sous-ensembles de l’espace ![]() [11].
[11].
Pour résumer ce que nous avons vu jusqu’à présent, la fonction de masse est déterminée a priori, sans nécessiter de considérations probabilistes. Elle peut correspondre à l’attribution, de façon subjective, de degrés de crédibilité en la réalisation des différents évènements envisageables sur ![]() , par un observateur.
, par un observateur.
L’attribution des valeurs de ![]() sert à exprimer le degré avec lequel l’expert ou l’observateur juge que chaque hypothèse est susceptible de se réaliser. Ainsi,
sert à exprimer le degré avec lequel l’expert ou l’observateur juge que chaque hypothèse est susceptible de se réaliser. Ainsi, ![]() décrit son imprécision relativement à ces degrés.
décrit son imprécision relativement à ces degrés.
3.2.3 La règle de combinaison de Dempster
Si nous revenons à la figure 3.2, nous constatons que le problème qui se pose est la fusion d’information, consistant à combiner des informations hétérogènes issues de plusieurs sources afin d’améliorer la prise de décision [3].
Voyons à présent un outil formel développé dans le cadre du modèle des croyances transférables permettant la fusion d’information. Nous posons l’hypothèse que les sources sont distinctes [16][21][22][23] par analogie avec l’indépendance des variables aléatoires en statistique.
Il peut arriver que pour la même hypothèse, deux capteurs apportent une information complètement différente. D’un point de vue formel, lors de la combinaison de deux fonctions de masse de croyance ![]() et
et ![]() , l’intersection entre les éléments focaux peut être vide. La fonction de masse de croyance résultat dans cette combinaison sera non nulle sur l’ensemble vide. Cette valeur quantifie alors la discordance entre les sources de croyance, et est appelée conflit [17]. Une normalisation peut être effectuée, ramenant la règle de combinaison conjonctive à la règle orthogonale de Dempster [6][7] (notée
, l’intersection entre les éléments focaux peut être vide. La fonction de masse de croyance résultat dans cette combinaison sera non nulle sur l’ensemble vide. Cette valeur quantifie alors la discordance entre les sources de croyance, et est appelée conflit [17]. Une normalisation peut être effectuée, ramenant la règle de combinaison conjonctive à la règle orthogonale de Dempster [6][7] (notée ![]() ) utilisée dans le modèle de Shafer [15][18] :
) utilisée dans le modèle de Shafer [15][18] :
(3.2.3.1) 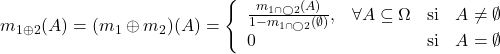
Une autre façon d’écrire cette règle de combinaison est :
(3.2.3.2) ![]()
Avec, pour mesure du conflit entre les sources :
(3.2.3.3) ![]()
3.2.4 Un affaiblissement simple
La règle d’affaiblissement simple pour intégrer la fiabilité des sources. L’application de la règle de combinaison disjonctive peut s’avérer trop conservatrice lorsque les sources de fonctions de masse de croyance ne sont pas fiables. Elle peut ainsi mener à une fonction de masse de croyance complètement non-informative (vide). Dans certaines applications, il est cependant possible de quantifier la fiabilité ce qui permet d’appliquer une règle de combinaison moins conservatrice dans le cas de sources non fiables.
La prise en compte de la fiabilité dans le cadre des fonctions de croyance porte le nom d’affaiblissement car le processus consiste à pondérer la masse des éléments d’une fonction de masse de croyance. Les premiers travaux sur l’affaiblissement dans le cadre des fonctions de croyance ont été développés par Shafer [15], axiomatisés par Smets [16] et généralisés par Mercier et Denœux [12]. L’affaiblissement généralisé a été appelé affaiblissement contextuel.
L’affaiblissement simple de Shafer d’une fonction de masse de croyance ![]() est défini comme la pondération de chaque masse
est défini comme la pondération de chaque masse ![]() de la distribution par un coefficient
de la distribution par un coefficient ![]() appelé fiabilité et où
appelé fiabilité et où ![]() est le taux d’affaiblissement.
est le taux d’affaiblissement.
(3.2.4.1) ![]()
Par le principe du minimum d’information (entropie maximale), le reste de la masse (après pondération) est transféré sur l’élément d’ignorance ![]() . Plus la source est fiable (et plus le taux d’affaiblissement
. Plus la source est fiable (et plus le taux d’affaiblissement ![]() est faible), moins la fonction de masse de croyance est modifiée alors que, plus la fiabilité diminue, plus la fonction de masse de croyance issue de l’affaiblissement tend vers la fonction de masse de croyance vide.
est faible), moins la fonction de masse de croyance est modifiée alors que, plus la fiabilité diminue, plus la fonction de masse de croyance issue de l’affaiblissement tend vers la fonction de masse de croyance vide.
3.3 La décision pignistique
A partir de l’ensemble des fonctions de croyance fournies par tous les capteurs, et suite à leur combinaison par la règle de Dempster, nous obtenons une fonction de croyance unique pour chacune des hypothèses possibles modélisant la connaissance du système. Il faut ensuite, à partir de cette connaissance, prendre une décision sur l’une des hypothèses.
Notons que les hypothèses du système ne représentent pas forcément les seules classes possibles (i.e. les 26 lettres de notre alphabet). Il est également possible de créer une nouvelle hypothèse qui correspondrait à l’évènement « aucune des hypothèses connues ». On parle alors de rejet, c’est à dire que l’individu inconnu n’est pas réinjecté dans la chaîne, il est tout simplement classé comme « impossible à reconnaître ». La mesure du conflit des capteurs lors de la fusion de Dempster (voir l’equation 3.2.3.3) est aussi une mesure sur laquelle le système peut se baser pour rejeter l’individu.
Les systèmes de fusion d’information, qu’ils soient basés sur la théorie des probabilités, des possibilités ou des fonctions de croyance, ont pour finalité la prise de décision et l’analyse de cette décision. Prendre une décision consiste à choisir une hypothèse sur un cadre de pari, généralement le cadre de discernement ![]() . La prise de décision peut être réalisée de façon automatique ou laissée à la responsabilité de l’utilisateur final (par exemple dans le cas de de l’aide au diagnostique dans le domaine de la Médecine).
. La prise de décision peut être réalisée de façon automatique ou laissée à la responsabilité de l’utilisateur final (par exemple dans le cas de de l’aide au diagnostique dans le domaine de la Médecine).
Dans le cadre du modèle des croyances transférables, la phase de décision s’appuie sur la distribution de probabilités pignistiques notée ![]() à partir de la distribution de masse
à partir de la distribution de masse ![]() [19]. La transformée pignistique consiste à répartir de manière équiprobable la masse d’une proposition
[19]. La transformée pignistique consiste à répartir de manière équiprobable la masse d’une proposition ![]() sur les hypothèses contenues dans
sur les hypothèses contenues dans ![]() .
.
(3.3.1) ![]()
(3.3.2) 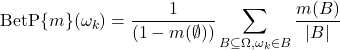
La décision est généralement prise en choisissant l’élément ![]() possédant la plus grande probabilité pignistique :
possédant la plus grande probabilité pignistique :
(3.3.3) ![]()
L’agent qui se base sur la transformée pignistique lors de la phase de prise de décision présente un comportement rationnel en maximisant l’utilité espérée. Alternativement, les plausibilités et les crédibilités peuvent être utilisées lorsque l’agent présente une attitude plutôt optimiste ou pessimiste.
Dans le cas des plausibilités, on dit que l’agent a une attitude optimiste dans le sens où la plausibilité d’un élément représente la valeur maximale de la masse de croyance sur cet élément qui pourrait être atteinte si des informations supplémentaires parvenaient au système de fusion (ce dernier utilisant la combinaison conjonctive pour intégrer cette nouvelle information). La distribution de probabilités sur les singletons à partir de laquelle une décision peut être prise est alors donnée ![]() par :
par :
(3.3.4) ![]()
Notons que la plausibilité d’un singleton ![]() est égale à sa communalité
est égale à sa communalité ![]() . De la même manière, un critère adapté à un agent « pessimiste » peut être obtenu en utilisant les crédibilités. La crédibilité d’un singleton
. De la même manière, un critère adapté à un agent « pessimiste » peut être obtenu en utilisant les crédibilités. La crédibilité d’un singleton ![]() est simplement égale à sa masse après normalisation de la fonction de masse de croyance
est simplement égale à sa masse après normalisation de la fonction de masse de croyance ![]() . Remarquons que pour tout élément
. Remarquons que pour tout élément ![]() :
:
(3.3.5) ![]()
et en particulier lorsque les plausibilités et les crédibilités sont calculées sur les singletons.
Pour le problème de prise de décision, nous supposons avoir une fonction de croyance ![]() sur
sur ![]() qui résume l’ensemble des informations apportées sur la valeur de la variable
qui résume l’ensemble des informations apportées sur la valeur de la variable ![]() . La décision consiste à choisir une action
. La décision consiste à choisir une action ![]() parmi un ensemble fini d’actions
parmi un ensemble fini d’actions ![]() . Une fonction de perte
. Une fonction de perte ![]() est supposée définie de telle manière que
est supposée définie de telle manière que ![]() représente la perte encourue si l’action
représente la perte encourue si l’action ![]() est choisie lorsque
est choisie lorsque ![]() . A partir de la probabilité pignistique, chaque action
. A partir de la probabilité pignistique, chaque action ![]() peut être associée à un risque défini comme le coût espéré relatif à
peut être associée à un risque défini comme le coût espéré relatif à ![]() si
si ![]() est choisie :
est choisie :
(3.3.6) ![]()
L’idée consiste ensuite à choisir l’action qui minimise ce risque, généralement appelé risque pignistique. En reconnaissance de formes, ![]() est l’ensemble des classes et les éléments de
est l’ensemble des classes et les éléments de ![]() sont généralement les actions
sont généralement les actions ![]() qui consistent à assigner le vecteur inconnu à la classe
qui consistent à assigner le vecteur inconnu à la classe ![]() .
.
Il est démontré que la minimisation du risque pignistique ![]() conduit à choisir la classe
conduit à choisir la classe ![]() de plus grand probabilité pignistique [8]. Si une action supplémentaire de rejet
de plus grand probabilité pignistique [8]. Si une action supplémentaire de rejet ![]() de coût constant
de coût constant ![]() est possible, alors le vecteur est rejeté si
est possible, alors le vecteur est rejeté si ![]() .
.
3.4 Prise de décision à partir de fonctions de croyance
Voyons à présent comment construire, en vue de la prise de décision, les fonctions de croyances sur les différentes hypothèses à partir de la précision des attributs, de la précision des classifieurs et des données en sortie de l’étage de classification.
Au niveau crédal du modèle des croyances transférables, afin d’obtenir les fonctions de croyance à partir des données d’apprentissage, deux familles de techniques sont généralement utilisées : les méthodes basées sur la vraisemblance qui utilisent l’estimation des densités et une méthode basée sur la distance dans laquelle les jeux de masses sont construits directement à partir des distances aux vecteurs d’apprentissage.
- Méthodes basées sur la vraisemblance.
Les densités de probabilités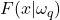 conditionnellement aux classes
conditionnellement aux classes 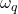 sont supposée connues. En ayant observé
sont supposée connues. En ayant observé 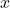 , la fonction de vraisemblance
, la fonction de vraisemblance 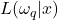 est une fonction de
est une fonction de 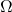 dans
dans 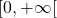 définie par
définie par 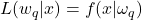 , pour tout
, pour tout ![Rendered by QuickLaTeX.com q\in[1,...,Q]](https://www.a2d.ai/wp-content/ql-cache/quicklatex.com-74c35124316d55b1e1f6dfdbd13b55eb_l3.png) . A partir de
. A partir de 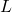 , Shafer [15] a proposé de construire une fonction de croyance sur
, Shafer [15] a proposé de construire une fonction de croyance sur 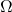 définie par sa fonction de plausibilité comme :
définie par sa fonction de plausibilité comme :
(3.4.1)
![Rendered by QuickLaTeX.com \begin{eqnarray*} pl(A)=\frac{\max_{\omega_q\in A}[L(\omega_q|X)]}{\max_{q}[L(\omega_q|X)]} & \forall A\subseteq\Omega \end{eqnarray*}](https://www.a2d.ai/wp-content/ql-cache/quicklatex.com-23a4976f586904b7208cc8a87ca23773_l3.png)
A partir de considérations axiomatiques, Appriou [1] a proposé une autre méthode basée sur la construction de
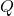 fonctions de croyances
fonctions de croyances 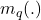 . L’idée consiste à prendre en compte de manière séparée chaque classe et à évaluer le degré de croyance accordé à chacune d’entre elles. Dans ce cas, les éléments focaux de chacune des fonctions de croyance
. L’idée consiste à prendre en compte de manière séparée chaque classe et à évaluer le degré de croyance accordé à chacune d’entre elles. Dans ce cas, les éléments focaux de chacune des fonctions de croyance 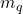 sont les singletons
sont les singletons 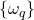 , les sous ensembles complémentaires
, les sous ensembles complémentaires 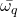 et
et 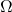 . Appriou obtient ainsi deux modèles différents :
. Appriou obtient ainsi deux modèles différents :Ici,
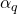 est un coefficient qui peut-être utilisé pour modéliser une information complémentaire (comme par exemple la fiabilité d’un capteur), et
est un coefficient qui peut-être utilisé pour modéliser une information complémentaire (comme par exemple la fiabilité d’un capteur), et 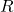 est une constante de normalisation qui est choisie dans
est une constante de normalisation qui est choisie dans ![Rendered by QuickLaTeX.com ]0,(\sup_x \max_q(L(\omega_q|x)))^{-1}]](https://www.a2d.ai/wp-content/ql-cache/quicklatex.com-59da6517126b2539ccc3ca241a513597_l3.png) . En pratique, les performances de ces deux modèles semblent être équivalentes. Cependant, Appriou recommande l’utilisation du modèle 2 qui a l’avantage d’être consistant avec le « théorème de Bayes généralisé » proposé par Smets dans [16]. A partir de ces
. En pratique, les performances de ces deux modèles semblent être équivalentes. Cependant, Appriou recommande l’utilisation du modèle 2 qui a l’avantage d’être consistant avec le « théorème de Bayes généralisé » proposé par Smets dans [16]. A partir de ces 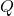 fonctions de croyance et en utilisant la règle de combinaison de Dempster, une fonction de croyance unique
fonctions de croyance et en utilisant la règle de combinaison de Dempster, une fonction de croyance unique 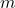 est obtenue par
est obtenue par  .
. - Méthode basée sur la distance.
La seconde famille de modèles se base sur des informations de distance. Dans cette dernière, citons comme exemple l’extension de l’algorithme des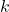 plus proches voisins qui a été introduit par T. Denœux dans [18]. Dans cette méthode, une fonction de croyance
plus proches voisins qui a été introduit par T. Denœux dans [18]. Dans cette méthode, une fonction de croyance 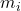 est directement construite en utilisant les informations apportées par les vecteurs
est directement construite en utilisant les informations apportées par les vecteurs 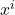 situés dans le voisinage du vecteur inconnu
situés dans le voisinage du vecteur inconnu 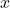 par :
par :
(3.4.4)
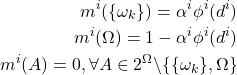
où
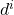 est la distance euclidienne du vecteur inconnu au vecteur
est la distance euclidienne du vecteur inconnu au vecteur 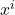 ,
, 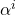 un paramètre associé au
un paramètre associé au 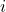 -ème voisin et
-ème voisin et 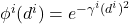 avec
avec 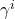 un paramètre positif (rappelons que l’opérateur
un paramètre positif (rappelons que l’opérateur 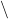 signifie « privé de »). La méthode des
signifie « privé de »). La méthode des 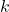 plus proches voisin permet d’obtenir
plus proches voisin permet d’obtenir 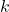 fonctions de croyance à agréger par la règle de combinaison pour la prise de décision.
fonctions de croyance à agréger par la règle de combinaison pour la prise de décision.
4 Proposition
4.1 Principe
La théorie de l’évidence présente plusieurs éléments d’intérêt dans notre quête d’une mesure de la précision associée à la décision, ainsi que dans l’intégration d’une telle mesure dans cette prise de décision. Le premier d’entre eux est certainement celui de pouvoir proposer un bornage pessimiste et optimiste de la décision, ce qui peut en première instance être rapproché de la tolérance souhaitée en association avec la décision. Le second correspond ensuite à l’introduction du facteur d’affaiblissement dans le propos. Par son entremise, il est possible d’intégrer un facteur prenant en compte la fiabilité de l’opérateur fournissant l’information. Cette fiabilité, ou confiance, est déduite d’un apprentissage effectué au préalable, c’est à dire hors ligne. Or tel qu’est construite l’approche, quelque soit la valeur établie, quelque soit l’objet à partir duquel est établie la mesure, celle ci sera considérée au même niveau d’importance que toutes celles issues de l’opérateur.
Il ne faut pas voir ici une critique de la construction du facteur d’affaiblissement qui a été introduit pour permettre la combinaison de différentes sources d’information, tels que des capteurs ou des bandes de fréquences dans des IRM. Derrière cette proposition se place l’hypothèse de linéarité de comportement de la source d’information face au bruit et/ou à l’information à acquérir. Cette hypothèse certainement valide dans le contexte où a été développée cette théorie n’est en revanche pas valide dans notre contexte plus générique.
Deux solutions s’offrent à nous pour développer notre proposition, la première serait d’intégrer un second facteur dans la formulation qui ne serait dépendant que de l’objet à mesurer au travers de l’opérateur ![]() . La seconde solution consiste à ne conserver qu’un seul facteur d’affaiblissement intégrant les deux aspects à prendre en compte :
. La seconde solution consiste à ne conserver qu’un seul facteur d’affaiblissement intégrant les deux aspects à prendre en compte :
- L’apport du type d’information considéré dans la prise de décision. Ce qui correspond à une pertinence a priori, c’est à dire uniquement liée à l’opérateur et considérée à la suite de l’apprentissage avant la phase de prise de décision proprement dite (phase dite en ligne).
- La qualité de la mesure, que nous appelons précision. Cette mesure de précision est directement dépendante de l’objet à mesurer vu au travers de l’opérateur, mesure effectuée pour prendre en compte les non linéarités de comportement de l’opérateur ou du capteur (i.e. cas des réponses en fonction des différent tissus dans l’imagerie médicale). Cette mesure de précision sera donc appelée mesure de précision a posteriori car établie à l’issu de la mesure.
Dans les deux cas, nous proposons de conserver l’écriture d’Appriou. La combinaison des différents éléments d’affaiblissement étant écrite sous forme multiplicative. Pour des raisons de temps nécessaire, nous n’avons pas associé dans ce travail ces deux parties liées à l’estimation de la précision totale (a priori et a posteriori). Entre autre raison à cette décision intervient notamment la problématique de l’estimation de la précision a priori, fortement dépendante de la construction de la base d’apprentissage.
Voyons à présent une partie des pistes envisagées pour cette question dans le cadre de la classification. Néanmoins, la littérature sur le sujet étant déjà importante, nous avons estimé qu’il existait déjà de nombreuses bases de réponse à cette question.
4.2 Mise en œuvre
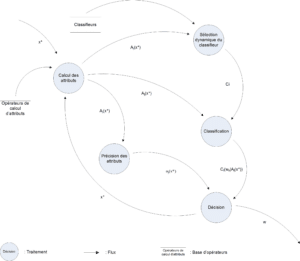
Les fonctions de croyances par classe/classifieur/attribut sont combinées (Dempster) afin de construire une fonction de croyance par classe. La prise de décision est ensuite faite selon l’équation 3.3.3. Le mécanisme de décision, est schématisé par la figure 4.2.1. Cette figure représente l’enchaînement des processus ainsi que les échanges entre eux. Nous avons représenté ici chacune des variables du formalisme, son origine et sa destination. La source du flux illustrant l’individu à analyser (![]() ) n’est pas représentée car nous ne traitons pas de cette partie.
) n’est pas représentée car nous ne traitons pas de cette partie. ![]() peut être un objet injecté directement dans le processus, mais il peut être issu de traitements postérieurs.
peut être un objet injecté directement dans le processus, mais il peut être issu de traitements postérieurs.
L’exploitation de l’expression d’Appriou, et notre version modifiée de l’expression d’Appriou exploite des étiquettes discrètes basées sur la fonction de vraisemblance ![]() liant un individu
liant un individu ![]() à son appartenance à la classe
à son appartenance à la classe ![]() .
.
Afin d’obtenir ces fonctions et selon le schéma de la figure 4.2.2 ces étiquettes sont dans notre cas issues d’un étage de classification liant l’individu à la classe ![]() . Classiquement dans ce cadre, la fonction de vraisemblance
. Classiquement dans ce cadre, la fonction de vraisemblance ![]() est alors liée à la distance
est alors liée à la distance ![]() de l’individu
de l’individu ![]() à la classe
à la classe ![]() selon le classifieur
selon le classifieur ![]() (suivant le classifieur, la distance peut être remplacée par un degré d’appartenance ou une probabilité). Cependant, la capacité d’associer un individu à une étiquette par un classifieur est dépendante du jeu d’attributs utilisé. De la même façon, chaque classifieur propose un partitionnement différent de l’espace des attributs en fonction du modèle de classe utilisé ou des métriques mises en œuvre. Notre écriture reliera donc la fonction de vraisemblance
(suivant le classifieur, la distance peut être remplacée par un degré d’appartenance ou une probabilité). Cependant, la capacité d’associer un individu à une étiquette par un classifieur est dépendante du jeu d’attributs utilisé. De la même façon, chaque classifieur propose un partitionnement différent de l’espace des attributs en fonction du modèle de classe utilisé ou des métriques mises en œuvre. Notre écriture reliera donc la fonction de vraisemblance ![]() à la distance
à la distance ![]() , où
, où ![]() représente le vecteur d’attributs fourni par l’opérateur
représente le vecteur d’attributs fourni par l’opérateur ![]() (moments de Zernike à l’ordre 15 par exemple ou histogramme couleur sur 32 bins obtenu par fuzzy C-means etc.) et
(moments de Zernike à l’ordre 15 par exemple ou histogramme couleur sur 32 bins obtenu par fuzzy C-means etc.) et ![]() faisant référence au classifieur
faisant référence au classifieur ![]() .
.
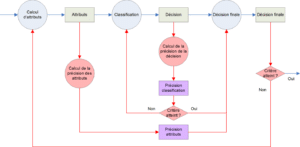
Le choix de cette écriture nous permet dés lors de combiner plusieurs étiquettes issues de classifieurs différents et/ou d’attributs différents. Selon le protocole choisi, les différents classifieurs seront mis en compétition directement ou une étape de sélection dynamique du meilleur d’entre eux sera opérée avant cette étape de fusion. Dans ce dernier cas, la compétition fusionne les étiquettes issues de différents attributs vus au travers du meilleur classifieur pour chacun d’entre eux. L’expression à laquelle nous aboutissons est directement déduite de l’équation 3.3.3 :
(4.2.1) ![Rendered by QuickLaTeX.com \begin{eqnarray*} \left\{ \begin{array}{ll} m_{ijq}(\{\omega_q\})&=0\\ m_{ijq}(\overline{\omega_q})&=\alpha_{jq}(1-R_{ijq}.C_i(\omega_q|A_j(x)))\\ m_{ijq}(\Omega)&=1-m_{ijq}(\overline{\omega_q})\\ \end{array} \right.\\ \nonumber\forall {i}\in[1,n_c], \forall {j}\in[1,n_a], \forall {q}\in[1,n_q] \end{eqnarray*}](https://www.a2d.ai/wp-content/ql-cache/quicklatex.com-e36fc3ef316a9113c3971284921a8717_l3.png)
Appriou intègre ![]() , un paramètre de normalisation de la formule établit pour que la masse de croyance
, un paramètre de normalisation de la formule établit pour que la masse de croyance ![]() soit comprise entre 0 et 1.
soit comprise entre 0 et 1. ![]() est donc une valeur comprise entre
est donc une valeur comprise entre ![]() et la valeur maximale qui peut être estimée pour
et la valeur maximale qui peut être estimée pour ![]() . Cette valeur de
. Cette valeur de ![]() est unique pour le classifieur
est unique pour le classifieur ![]() et correspond à la plus grande distance identifiée ou possible entre un individu et les classes définies pour ce classifieur, d’où :
et correspond à la plus grande distance identifiée ou possible entre un individu et les classes définies pour ce classifieur, d’où :
(4.2.2) 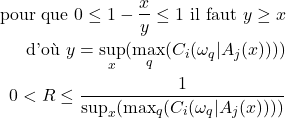
La masse de croyance que nous venons d’établir est ![]() , c’est à dire la masse de croyance associée au fait que la classe
, c’est à dire la masse de croyance associée au fait que la classe ![]() soit attribuée à l’individu
soit attribuée à l’individu ![]() par le classifieur
par le classifieur ![]() pour le vecteur d’attributs
pour le vecteur d’attributs ![]() . Or, ce qui nous intéresse c’est la décision d’affectation finale de la classe
. Or, ce qui nous intéresse c’est la décision d’affectation finale de la classe ![]() à l’individu
à l’individu ![]() et par voie de conséquence la masse de croyance en la classe
et par voie de conséquence la masse de croyance en la classe ![]() ,
, ![]() , et les masses associée
, et les masses associée ![]() et
et ![]() :
:
(4.2.3) ![Rendered by QuickLaTeX.com \begin{eqnarray*} \left\{ \begin{array}{l} m_q(\{\omega_q\})\\ m_q(\overline{\omega_q})\\ m_q(\Omega) \end{array} \right.\\ \nonumber\forall q\in[1,n] \end{eqnarray*}](https://www.a2d.ai/wp-content/ql-cache/quicklatex.com-ccdf35491aee4ebb5e3a9bbb9f3c68ce_l3.png)
A partir du modèle de combinaison de Dempster, nous formalisons cette prise de décision à partir des ![]() décisions intermédiaires sur un ensemble de
décisions intermédiaires sur un ensemble de ![]() étiquettes pour un jeu unique d’attributs :
étiquettes pour un jeu unique d’attributs :
(4.2.4) ![Rendered by QuickLaTeX.com \begin{eqnarray*} \left\{ \begin{array}{ll} m(\{\omega_k\})&=\bigoplus_{q=1}^{n_q}m_{iq}(\{\omega_k\})\\ m(\overline{\omega_k})&=\bigoplus_{q=1}^{n_q}m_{iq}(\overline{\omega_k}) \end{array} \right.\\ \nonumber\forall q\in[1,n], \forall i\in[1,n_c] \end{eqnarray*}](https://www.a2d.ai/wp-content/ql-cache/quicklatex.com-70ad84b60c2beea20bc4699b6f17f4e5_l3.png)
et :
(4.2.5) ![]()
De façon plus générale, en présence de plusieurs jeux d’attributs issus d’opérateurs différents (ou paramètres différents), la règle de combinaison de Dempster nous permet d’aboutir à la formulation générale :
(4.2.6) ![]()
Le diagramme de flots de données de la figure 4.2.1 illustre le fonctionnement de cette écriture.
Bibliographie
[1] A. Appriou. Probabilités et incertitudes en fusion de données multi-senseurs. Revue Scientifique et Technique de la Défense, 11 :27–40, 1991.
[2] D. Arrivault. Apport des graphes dans la reconnaissance non-contrainte de caractères manuscrits anciens. PhD thesis, Université de Poitiers, 2002.
[3] I. Bloch. Fusion d’informations numériques : panorama méthodologique. In Journées Nationales de la Recherche en Robotique, 2005.[7]
[4] R. Caruana and A. Niculescu-Mizil. An empirical comparison of supervised learning algorithms. In ICML ’06 : Proceedings of the 23rd international conference on Machine learning, pages 161–168, New York, NY, USA, 2006. ACM.
[5] T. M. Cover and P. E. Hart. Nearest neighbor pattern classification. IEEE Trans. on Information Theory, 13(1) :21–27, 1967.
[6] A. P. Dempster. Upper and lower probabilities induced by multiple valued mappings. Annals of Mathematical Statistics, 38 :325–339, 1967.
[7] A. P. Dempster. A generalization of bayesian inference. Journal of the Royal Statistical Society, 30 :205–247, 1968.
[8] T. Denœux. Analysis of evidence-theoretic decision rules for pattern classification. Pattern Recognition, 30(7) :1095–1107, 1997.
[9] J. Kholas and P. A. Monney. Lecture Notes in Economics and Mathematical Systems, volume 425, chapter A mathematical theory of hints : An approach to the Dempster-Shafer theory of evidence. Springer-Verlag, 1995.
[10] G. J. Klir and M. J. Wierman. Uncertainty-based information. Elements of generalized information theory, 2nd edition. Studies in fuzzyness and soft computing. Physica-Verlag, 1999.
[11] E. Lefevre, O. Colot, and P. Vannoorenberghe. Belief function combination and conflict management. Information Fusion, 3 :149–162, 2002.
[12] D. Mercier, B. Quost, and T. Denoœux. Refined modeling of sensor reliability in the belief function framework using contextual discounting. Information Fusion, 2007.
[13] E. Ramasso. Reconnaissance de séquences d’états par le Modèle des Croyances Transférables – Application à l’analyse de vidéos d’athlétisme. PhD thesis, Université Joseph Fourier de Grenoble, 2007.
[14] I. Rish. An empirical study of the naive bayes classifier. In IJCAI-01 workshop on « Empirical Methods in AI », 2001.
[15] G. Shafer. A Mathematical Theory of Evidence. Princeton University Press, 1976.
[16] P. Smets. Beliefs functions : The disjunctive rule of combination and the generalized bayesian theorem. Int. Jour. of Approximate Reasoning, 9 :1–35, 1993.
[17] P. Smets. The nature of the unnormalized beliefs encountered in the transferable belief model. In Proceedings of the 8th Annual Conference on Uncertainty in Artificial Intelligence, pages 292–297, 1992.
[18] P. Smets. Advances in the Dempster-Shafer Theory of Evidence – What is Dempster-Shafer’s model ? Wiley, 1994.
[19] P. Smets. Decision making in the tbm : The necessity of the pignistic transformation. Int. Jour. of Approximate Reasoning, 38 :133–147, 2005.
[20] P. Smets and R. Kennes. The transferable belief model. Artificial Intelligence, 66(2) :191–234, 1994.
[21] B. Yaghlane, P. Smets, and K. Mellouli. Belief function independence : I. the marginal case. Int. Jour. of Approximate Reasoning, 29 :47–70, 2001.
[22] B. Yaghlane, P. Smets, and K. Mellouli. Belief function independence : II. the conditionnal case. Int. Jour. of Approximate Reasoning, 31(1) :31–75, 2002.
[23] B. Yaghlane, P. Smets, and K. Mellouli. Independence concept for belief functions. In Physica-Verlag, editor, Technologies for constructing intelligent systems : Tools, 2002.[93]