Comment mesurer la précision d’un classifieur ?
S. Sochacki, PhD in Computer Science
A2D, ZA Les Minimes, 1 rue de la Trinquette, 17000 La Rochelle, FRANCE
1 INTRODUCTION
Nous considérons toujours qu’une méthode, ne sera jamais optimale pour l’intégralité des individus qu’elle traitera. En métrologie par exemple, nous savons que la précision d’un capteur n’est pas constante sur la bande des valeurs qu’il peut accepter, comme l’illustre la figure 1.1 représentant l’évolution de la précision d’un capteur d’humidité et de température utilisé en météorologie. Nous voyons très nettement que la précision des mesures est plus faible sur les extrêmes.
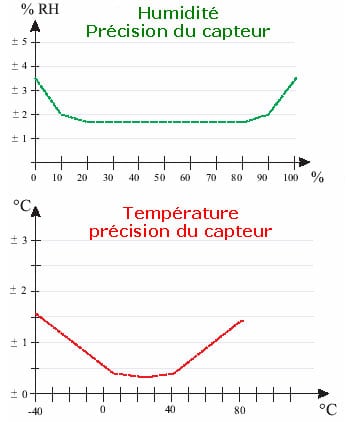
Afin de proposer à l’utilisateur une information sur la qualité de la décision, il nous faut prendre en compte toutes les mesures de précision possibles, relevées à chaque étape des traitements réalisés avant d’arriver à la décision finale. Concernant la classification, qu’y a t’il de mesurable en sortie d’un classifieur ? Est-ce sa précision ? Si oui, pouvons-nous à partir de cette mesure, sélectionner dynamiquement un classifieur afin d’optimiser les temps de calculs et la performance de la reconnaissance ?
Pour détailler nos travaux, voyons d’abord ce qu’est précisément un classifieur et quelles mesures peut-on réaliser sur un classifieur selon la littérature (partie 2). A partir de là, la partie 3 présente différentes façons de sélectionner dynamiquement un classifieur. Nous verrons ensuite les données avec lesquelles nous avons travaillé et nos différents résultats obtenus en partie 4. La partie 5 sera consacrée à l’étude de ces résultats et la partie 6 à la conclusion de cet article.
2 LES CLASSIFIEURS
Le Trésor de la Langue Française définit la classification comme la »répartition systématique en classes, en catégories, d’êtres, de choses ou de notions ayant des caractères communs notamment afin d’en faciliter l’étude ». Nous définirons donc un classifieur comme un outil automatique, un opérateur, réalisant une classification.
D’un point de vue mathématique, un classifieur est une application d’un espace d’attributs ![]() (discret ou continu) vers un ensemble d’étiquettes
(discret ou continu) vers un ensemble d’étiquettes ![]() .
.
Les classifieurs peuvent-être fixes ou apprenants, et ceux-ci peuvent à leur tour être divisés en classifieurs apprenants supervisés ou non supervisés.
Les applications sont multiples. On en retrouve en médecine (analyse des tests pharmacologiques, analyse de données d’IRM), en finance (prédiction de cours), en téléphonie mobile (décodage de signal, correction d’erreurs), en vision artificielle (reconnaissance de visages, suivi de cible), en reconnaissance de la parole, en datamining (analyse des achats en supermarché) et encore dans bien d’autres domaines.
Nous pouvons citer en exemple un classifieur qui prend en entrée les salaires d’une personne, son âge, son statut marital, son adresse et ses relevés bancaires, et qui classifie une personne comme recevable/non-recevable à l’obtention d’un crédit.
Un classifieur se base sur une connaissance a priori (fixée par l’expert ou construite par apprentissage) décrivant les différentes classes dans l’espace des attributs. A partir de cette connaissance, le classifieur va attribuer, aux individus inconnus qui lui seront présentés, le label de la classe à laquelle l’individu à la plus forte probabilité d’appartenir.
Il faut savoir qu’un classifieur seul ne peut assurer des performances idéales pour tous les cas possibles (modèles de classes se recouvrant, individu aux frontières entre plusieurs classes etc.). C’est pour cela qu’il est intéressant de combiner plusieurs classifieurs afin qu’ils compensent leurs erreurs entre eux.
Zouari propose une taxonomie (voir figure 2.1) de différentes méthodes de combinaison dans [38].
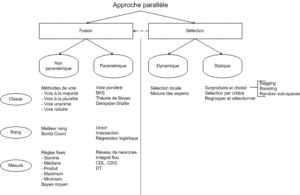
Elle rapporte notamment les travaux de Parker[26] qui montrent que les méthodes de type rang peuvent être plus performantes que les méthodes de type classe et mesure. Elle explique aussi que les méthodes non-paramétriques sont les plus utilisées par les chercheurs car simples à mettre en œuvre et n’utilisant pas de traitements supplémentaires (apprentissage). Nous ajouterons à cela qu’elles sont souvent les plus rapidement codées et surtout indépendantes des structures de classes.
Le but de la classification est d’établir des relations d’ordre entre les individus, afin d’obtenir une information la plus concise possible, atteindre le niveau d’abstraction le plus important (i.e. décrire, de manière précise, un document de 3Mo en 100ko). Il existe un espace qui décrive les données connues mais comment le choisir ?
Un classifieur peut être vu d’une part comme une mesure de distance, et d’autre part comme une méthode d’organisation spatiale (avec en fond une méthode d’optimisation). Ces deux parties combinées font de l’opérateur de classification un opérateur de pavage de l’espace de représentation des données qui lui sont proposées. Ceci entraîne des questions telles que, compte tenu d’une distance, quelle est la meilleure organisation ?
Le rôle du classifieur est double :
- Analyser les données sans apprentissage (sans supervision) : créer des groupes, mettre en place une organisation ;
- Positionner les individus par rapport à des groupes avec apprentissage (avec supervision) : information locale autour de l’individu.
De façon plus générale, nous voulons créer des groupes répondant à des attentes d’usage ou d’interprétation, les créer artificiellement selon des caractères communs, le choix des critères contraignant le choix de l’espace. Mais comment choisit-on ces critères ?
Les techniques de classification automatique produisent des groupements d’objets (ou individus) décrits par un certain nombre de
variables ou de caractères (les attributs). Le recours à de telles techniques est souvent lié à des suppositions sinon à des exigences
sur les regroupements des individus. Il existe plusieurs familles d’algorithmes de classification, comme nous pouvons le trouver dans[22] :
- Les algorithmes de partitionnement
- Les algorithmes ascendants (agglomératifs)
- Les algorithmes descendants (divisifs)
Ces méthodes présentent chacune des avantages et des inconvénients différents qui sont à l’origine de leur sélection en fonction du contexte applicatif. Bien évidement, ces aspects justifient également l’utilisation combinée de classifieurs. Toute une communauté organisée autour du monde de l’apprentissage s’est ainsi constituée pour combiner plusieurs classifieurs dans une même application. Cependant, dans notre contexte, ces combinaisons sont définies comme statiques, car établies a priori de la décision finale, à l’issue de l’apprentissage.
Sans reprendre l’argumentaire induisant qu’un même opérateur peut avoir du mal à être adapté à l’ensemble des cas de figure posés par l’application, nous aboutissons ici également au même propos concernant les combinaisons statiques de classifieurs. Il est bien entendu que ceci n’est pas une vérité absolue, la qualité des résultats obtenus par ces techniques de combinaison statique de classifieurs pour certaines applications n’étant pas à remettre en cause. Cependant, dans le cadre d’applications où la variabilité des données est très grande, l’assemblage statique peut avoir du mal à atteindre un haut niveau de résultat.
Dans l’hypothèse de la combinaison dynamique de classifieurs, nous savons que se posent à la fois les questions de sélection dynamique du meilleur classifieur et dans notre réflexion celles de l’estimation d’une mesure de précision à associer au résultat de la classification.
Pour démarrer l’étude de ces questions, nous nous appuierons sur les travaux de L. Kuncheva[20][18][19] qui a étudié et développé un ensemble d’outils de mesure de la qualité d’un classifieur par rapport à d’autres classifieurs, puis présente une mesure (la diversité) de l’apport d’un classifieur dans un groupe de classifieurs.
2.1 MESURE DE LA QUALITÉ DANS LA LITTÉRATURE
L’estimation de la qualité des résultats issus d’un classifieur s’appuie bien souvent sur l’analyse a posteriori de la propension des classifieurs à se tromper. Lors d’analyse comparatives de classifieurs entre eux, la qualité est estimée en fonction du taux de bonne classification. Ces comparaisons peuvent se faire sur les mêmes critères que pour un seul classifieur (bonnes/mauvaises reconnaissances etc.), mais également utiliser des outils, inspirés des statistiques, de mesure de la qualité d’un modèle, d’une loi de probabilité etc.
Dans la recherche de ce qui pourrait constituer une estimation de la précision de décision ou des éléments entrant dans la combinaison dynamique des classifieurs, nous avons analysé différents critères associés à la qualité de la décision. Nous proposons ci-après quelques uns de ces critères :
- Le calcul de l’erreur d’un classifieur, qui correspond au nombre d’individus mal rangés sur le nombre d’individus total. Exprimé sous forme de probabilité, il devient possible de sélectionner les classifieurs selon leur probabilité de faire une erreur dans un intervalle de confiance.
- La comparaison entre 2 classifieurs : si 2 classifieurs donnent des taux d’erreurs différents sur une même base de test, sont ils vraiment différents ?
- Soient 2 classifieurs, et leurs performances,
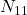 nombre d’individus correctement classés par les 2,
nombre d’individus correctement classés par les 2, 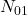 nombre d’individus mal classés par le premier mais bien classés par le second,
nombre d’individus mal classés par le premier mais bien classés par le second, 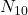 l’inverse et
l’inverse et 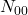 le nombre d’individus mal classés par les 2. Il existe une variable statistique suivant une loi de Chi-deux, mesurant la qualité d’un classifieur par rapport à un autre, s’écrivant :
le nombre d’individus mal classés par les 2. Il existe une variable statistique suivant une loi de Chi-deux, mesurant la qualité d’un classifieur par rapport à un autre, s’écrivant :
(2.1.1)
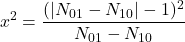
Sachant
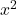 à peu près distribué selon
à peu près distribué selon 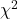 à 1 degré de liberté, on peut dire, avec un niveau de certitude de 0.05, que si
à 1 degré de liberté, on peut dire, avec un niveau de certitude de 0.05, que si 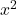 >3.841, alors les classifieurs présentent des performances fortement différentes. Notons qu’il existe aussi un test appelé « difference of two proportions » mais Dietterich prouve dans [4] que cette mesure est trop sensible à la violation de la règle d’indépendance des données (problème du jeu de données pour l’apprentissage et la reconnaissance restreint) et recommande d’utiliser la mesure ci-dessus.
>3.841, alors les classifieurs présentent des performances fortement différentes. Notons qu’il existe aussi un test appelé « difference of two proportions » mais Dietterich prouve dans [4] que cette mesure est trop sensible à la violation de la règle d’indépendance des données (problème du jeu de données pour l’apprentissage et la reconnaissance restreint) et recommande d’utiliser la mesure ci-dessus.
- Soient 2 classifieurs, et leurs performances,
- Plusieurs auteurs ont étendu cette analyse comparative au cas où plusieurs classifieurs sont combinés à partir de la même base d’apprentissage [35] :
- Le Q Test de Cochran[8][21] vérifie l’hypothèse : »tous les classifieurs présentent les même performances ». Si l’hypothèse est vérifiée alors
(2.1.2)
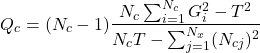
La variable
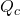 suit un
suit un 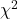 à
à 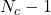 degrés de liberté, avec
degrés de liberté, avec 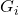 le nombre d’éléments de
le nombre d’éléments de 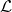 (espace d’apprentissage) correctement classés par le classifieur
(espace d’apprentissage) correctement classés par le classifieur 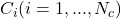 ,
, 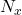 étant le nombre total d’individus appris.
étant le nombre total d’individus appris. 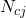 est le nombre total de classifieurs de
est le nombre total de classifieurs de 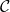 qui ont correctement classé l’objet
qui ont correctement classé l’objet 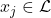 et
et 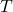 est le nombre total de bonnes décisions prises par l’ensemble des classifieurs.Ainsi, pour un niveau de confiance donné, si
est le nombre total de bonnes décisions prises par l’ensemble des classifieurs.Ainsi, pour un niveau de confiance donné, si 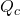 est supérieur à la valeur attendue du
est supérieur à la valeur attendue du 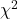 alors il existe des différences significatives entre les classifieurs justifiant leur combinaison.
alors il existe des différences significatives entre les classifieurs justifiant leur combinaison. - Le même principe peut être adopté en adoptant une loi de Fisher-Snedecor ayant
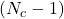 et
et 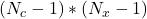 degrés de liberté. C’est le F-Test[23]. En partant des performances des classifieurs estimées au cours de l’apprentissage
degrés de liberté. C’est le F-Test[23]. En partant des performances des classifieurs estimées au cours de l’apprentissage 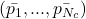 et la performance moyenne globale
et la performance moyenne globale 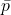 on obtient la somme des carrés pour les classifieurs :
on obtient la somme des carrés pour les classifieurs :
(2.1.3)
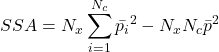
Puis la somme des carrés pour les objets :
(2.1.4)
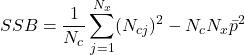
La somme totale des carrés :
(2.1.5)
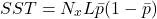
Enfin, la somme totale des carrés pour l’interaction classification/objet :
(2.1.6)
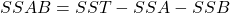
Dés lors, le critère
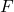 est estimé comme le rapport entre le MSA et le MSAB définis comme suit :
est estimé comme le rapport entre le MSA et le MSAB définis comme suit :(2.1.7)
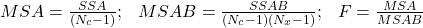
- Il est également possible d’appliquer une validation croisée[4]. Il s’agit de répéter un certain nombre de fois (
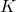 ) l’apprentissage/reconnaissance, en séparant à chaque fois le jeu de données à apprendre en 2 sous-jeux (habituellement 2/3 des données pour l’entraînement et 1/3 pour le test). Deux classifieurs
) l’apprentissage/reconnaissance, en séparant à chaque fois le jeu de données à apprendre en 2 sous-jeux (habituellement 2/3 des données pour l’entraînement et 1/3 pour le test). Deux classifieurs 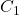 et
et 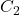 sont entraînés sur le jeu d’apprentissage et testés sur le jeu de test. A chaque tour, les précisions des deux classifieurs sont mesurées :
sont entraînés sur le jeu d’apprentissage et testés sur le jeu de test. A chaque tour, les précisions des deux classifieurs sont mesurées : 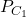 et
et 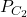 . Nous obtenons ainsi un ensemble de différences, de
. Nous obtenons ainsi un ensemble de différences, de  à
à 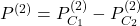 . En posant
. En posant 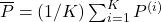 , nous mesurons :
, nous mesurons :
(2.1.8)
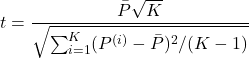
Si
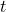 suit bien une loi de Student à
suit bien une loi de Student à 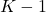 degrés de liberté (et pour le niveau de confiance choisi) alors les deux classifieurs présentent le même comportement.
degrés de liberté (et pour le niveau de confiance choisi) alors les deux classifieurs présentent le même comportement.
- Le Q Test de Cochran[8][21] vérifie l’hypothèse : »tous les classifieurs présentent les même performances ». Si l’hypothèse est vérifiée alors
Rappelons que l’optique de ce travail est d’aboutir à un système de sélection dynamique d’opérateur de classification, basé sur une mesure de qualité. Les méthodes présentées ci-dessus présentent un certain nombre d’inconvénients pour répondre à notre besoin :
- En ce qui concerne la mesure de l’erreur d’un classifieur, cette information est non uniforme sur l’espace des attributs. De plus, nous pouvons supposer que cette information variera si nous augmentons la taille de l’espace d’apprentissage dans le temps.
- Les méthodes de comparaison de classifieurs demandent un grand nombre de sessions d’entraînement et de test. Au delà des comparaisons, une fois la mesure établie, comment décider sur le classifieur à utiliser ? Dans le cas de la validation croisée, si nous réalisons 10 essais, nous construisons 10 classifieurs différents, construits sur 10 sous-ensembles différents. Ces méthodes ont pour seul but de donner une estimation de la précision d’un certain modèle construit uniquement sur le problème présent. Ainsi, Dietterich, dans [4], pose l’hypothèse selon laquelle la précision de la classification varie en fonction de la taille du jeu d’apprentissage.
Kuncheva propose pour cela une approche considérant un ensemble de classifieurs élémentaires comme un seul classifieur, construit et testé sur les mêmes jeux d’apprentissage et de test.
2.2 LA DIVERSITÉ : UNE SOLUTION ?
2.2.1 DÉFINITION
Il faut admettre que chaque classifieur commet des erreurs, car sinon quelle serait l’utilité de vouloir les combiner ? A partir de là, nous cherchons donc à compenser les erreurs d’un classifieur en le combinant avec un autre, qui produira des erreurs mais sur des objets différents. Ainsi, la diversité des sorties d’un classifieur devient un élément crucial pour réussir la combinaison. De façon intuitive, nous pouvons dire que, cherchant à obtenir une sortie de la meilleure qualité possible, s’il y a des erreurs, il vaut mieux que ces erreurs tombent sur des objets différents d’un classifieur à l’autre. Kuncheva explique qu’en pratique il est très difficile de définir une seule mesure de diversité, et encore plus compliqué de lier cette mesure à la performance de l’ensemble en une et simple expression de dépendance. Il existe des mesures de diversité propres à certaines branches de la science (biologie, conception de logiciels etc.), nous nous pencherons sur celles qui concernent les ensembles de classifieurs. La diversité peut être considérée de 3 points de vue différents :
- Comme caractéristique de l’ensemble des classifieurs : Nous avons un ensemble de classifieurs, mais nous ne savons pas quelle méthode de combinaison utiliser et nous ne savons même pas si les décisions données sont correctes. Dans ce cas, la diversité apporte des informations supplémentaires sur les taux d’erreurs individuels et sur l’erreur globale. La diversité permet de découvrir si un classifieur contribue ou non au succès de l’ensemble.
- Comme caractéristique de l’ensemble des classifieurs et de leur combinaison : Dans ce cas, nous connaissons l’ensemble des sorties. Ainsi nous pouvons dire quel classifieur dévie le plus et celui qui dévie le moins par rapport au reste de l’ensemble et mesurer la diversité sur une base plus individuelle. Différentes combinaisons amèneront à différentes diversités pour le même ensemble de classifieurs.
- Comme caractéristique de l’ensemble des classifieurs, de leur combinaison et des erreurs : nous pouvons enfin utiliser l’information connue a priori de la classe d’appartenance des individus du jeu d’apprentissage (cette information est aussi appelée oracle). La diversité est considérée comme un composant de l’ensemble des erreurs. C’est ce sur quoi portent actuellement les travaux de Kuncheva[19] : découvrir une relation entre la diversité et l’erreur de l’ensemble afin de construire de meilleures combinaisons.
Avant de découvrir diverses mesures de la diversité, rappelons les notations suivantes :
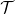 : Jeu de données,
: Jeu de données, 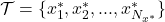
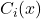 : décision du classifieur
: décision du classifieur 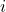 pour l’individu
pour l’individu 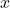
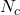 : Nombre de classifieurs
: Nombre de classifieurs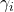 : précision ou probabilité pour le classifieur
: précision ou probabilité pour le classifieur 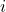 de donner la bonne réponse
de donner la bonne réponse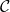 : espace des classifieurs
: espace des classifieurs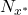 : nombre d’individus inconnus
: nombre d’individus inconnus
2.2.2 MESURE DE DIVERSITÉ PAR PAIRE DE CLASSIFIEUR
- Mesure de désaccord : probabilité que deux classifieurs ne soient pas d’accord sur leurs décisions
- Mesure de la double faute : probabilité que les classifieurs se trompent tous les deux
2.2.3 AUTRES MESURES DE DIVERSITÉ
- Mesure de l’entropie : considérant que l’ensemble est plus diversifié si pour un individu particulier, la moitié des votes est 0 et l’autre est 1, et de la même manière que la diversité est nulle si tous les classifieurs sont d’accord, une mesure possible de ce concept est :
(2.2.3.1)
![Rendered by QuickLaTeX.com \begin{equation*} E=\frac{1}{N_{x^*}}\frac{2}{N_c-1}\sum_{j=1}^{N_{x^*}}\min[(\sum_{i=1}^{N_c}C_{i}(x^*_j)),(N_c-\sum_{i=1}^{N_c}C_{i}(x^*_j))] \end{equation*}](https://www.a2d.ai/wp-content/ql-cache/quicklatex.com-7b0ae0f9d99441bc57723dc41574b9e1_l3.png)
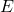 variant de 0 à 1 selon si tous les classifieurs donnent la même réponse, ou si la diversité est maximale.
variant de 0 à 1 selon si tous les classifieurs donnent la même réponse, ou si la diversité est maximale. - Variance de Kohavi-Wolpert : si le même classifieur est entraîné plusieurs fois (avec des jeux de données différents) et que la variance de sa décision est étudiée pour un même individu,
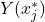 étant le nombre de votes corrects pour l’individu
étant le nombre de votes corrects pour l’individu 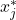 alors :
alors :
(2.2.3.2)
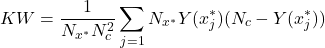
Notons que la mesure
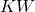 est proportionnelle à la moyenne des mesures de désaccord entre les classifieurs
est proportionnelle à la moyenne des mesures de désaccord entre les classifieurs 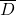 :
:(2.2.3.3)
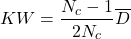
- Mesure du taux d’accord (Interrater Agreement) : connaissant la précision moyenne des classifieurs
(2.2.3.4)
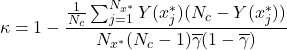
Notons la relation avec
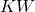 :
:(2.2.3.5)
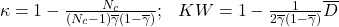
- Mesure de la difficulté : le principe est de définir une variable aléatoire discrète
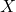 ayant valeur dans
ayant valeur dans 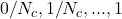 et de calculer la proportion de classifieurs de
et de calculer la proportion de classifieurs de 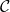 qui classifient correctement une entrée
qui classifient correctement une entrée 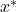 tirée aléatoirement de la distribution du problème. Les
tirée aléatoirement de la distribution du problème. Les 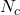 classifieurs de
classifieurs de 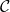 sont exécutés sur
sont exécutés sur 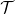 afin d’estimer la fonction de probabilité de
afin d’estimer la fonction de probabilité de 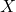 . L’analyse de la distribution de
. L’analyse de la distribution de 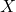 indiquera les individus qui posent le plus de difficultés à être reconnus. De plus, l’aspect général de cette distribution sera un indicateur de l’indépendance des classifieurs.
indiquera les individus qui posent le plus de difficultés à être reconnus. De plus, l’aspect général de cette distribution sera un indicateur de l’indépendance des classifieurs. - Diversité généralisée : soit
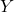 , une variable aléatoire exprimant la proportion des classifieurs qui « se trompent » sur un individu
, une variable aléatoire exprimant la proportion des classifieurs qui « se trompent » sur un individu 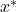 tiré aléatoirement
tiré aléatoirement 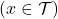 .
.
Soit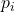 , la probabilité que
, la probabilité que 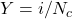 , soit la probabilité qu’il y ait exactement
, soit la probabilité qu’il y ait exactement 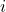 sur les
sur les 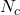 classifieurs qui échouent sur un individu tiré au hasard.
classifieurs qui échouent sur un individu tiré au hasard.
Soit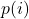 la probabilité que
la probabilité que 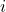 classifieurs tirés au hasard échouent sur un
classifieurs tirés au hasard échouent sur un 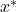 choisi aléatoirement.
choisi aléatoirement.
Supposons que nous choisissions 2 classifieurs au hasard dans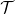 .
.
La diversité maximale est obtenue lorsqu’un des deux classifieurs échoue tandis que l’autre donne une bonne réponse. Dans ce cas, la probabilité que les deux classifieurs échouent est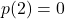 . La diversité minimale est obtenue lorsque l’échec d’un classifieur est systématiquement accompagné par l’échec du deuxième classifieur. Ainsi, la probabilité que les deux classifieurs se trompent est la même que la probabilité qu’un classifieur tiré aléatoirement échoue (soit
. La diversité minimale est obtenue lorsque l’échec d’un classifieur est systématiquement accompagné par l’échec du deuxième classifieur. Ainsi, la probabilité que les deux classifieurs se trompent est la même que la probabilité qu’un classifieur tiré aléatoirement échoue (soit 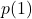 ). Sachant que
). Sachant que 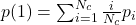 et
et 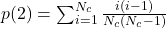 on obtient :
on obtient :
(2.2.3.6)
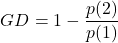
- Erreur commune ou Coincident Failure Diversity : cette mesure est simplement une modification de la diversité généralisée
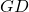 , afin d’obtenir une valeur minimale de 0 lorsque tous les classifieurs ont toujours raison, ou lorsqu’ils donnent tous simultanément soit une réponse juste, soit une réponse fausse :
, afin d’obtenir une valeur minimale de 0 lorsque tous les classifieurs ont toujours raison, ou lorsqu’ils donnent tous simultanément soit une réponse juste, soit une réponse fausse :
(2.2.3.7)
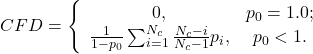
Ces mesures indiquent la diversité d’un groupe de classifieurs construit a priori, en se basant sur les apports (ou pénalités) des classifieurs entre eux. Or, nous cherchons à établir une mesure de la qualité ou de la précision en sortie de l’étape de classification. Kuncheva[19] établit une liste de relations entre la diversité et la qualité de la classification.
2.2.4 RELATION ENTRE DIVERSITÉ ET PERFORMANCE DE LA CLASSIFICATION
-
- « Plus la diversité est importante, plus l’erreur est faible »[19]
- Chaque classifieur peut-être représenté graphiquement par un point dans un espace bidimensionnel généré par « Sammon mapping »[29], la distance entre chaque point étant la diversité par paire. Il est possible d’y ajouter chaque ensemble de classifieur comme un classifieur à part entière et même l’oracle lui-même. En considérant que chaque point est une paire de classifieur,
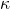 peut jouer le rôle d’abscisse, l’erreur moyenne des deux classifieurs pouvant dans ce cas être l’ordonnée. Ceci nous donne ainsi
peut jouer le rôle d’abscisse, l’erreur moyenne des deux classifieurs pouvant dans ce cas être l’ordonnée. Ceci nous donne ainsi 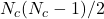 points, situant les meilleures paires dans la partie inférieur gauche (là où l’erreur est minimale et la diversité maximale) (voir figure 2.2.4.1)
points, situant les meilleures paires dans la partie inférieur gauche (là où l’erreur est minimale et la diversité maximale) (voir figure 2.2.4.1)
- Il est également possible de produire un grand ensemble de classifieurs pour n’en sélectionner que les plus diversifiés et les plus performants :
-
- La matrice de diversité portant l’ensemble des valeurs du critère de la double faute est créée, et un nombre donné de classifieurs est choisi parmi les moins représentés. Une sorte de « pruning » analogue peut être réalisé sur la valeur de
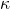 après utilisation de l’algorithme AdaBoost
après utilisation de l’algorithme AdaBoost - Il est possible, en considérant la matrice des doubles fautes comme matrice de distance, de créer des clusters de classifieurs. Ainsi groupés, les membres de chaque ensemble auront tendance à faire les mêmes erreurs alors que deux classifieurs choisis dans 2 groupes différents feront des erreurs sur des objets différents. A chaque étape de l’algorithme, un classifieur est sélectionné dans chaque cluster (i.e. celui possédant le plus fort taux de reconnaissance). Ainsi, au début, chaque classifieur est un groupe de lui-même (il y a donc
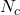 clusters), et ainsi l’ensemble est composé de tous les classifieurs. Ensuite, les deux classifieurs les moins diversifiés sont joints dans un cluster (l’ensemble se compose donc de
clusters), et ainsi l’ensemble est composé de tous les classifieurs. Ensuite, les deux classifieurs les moins diversifiés sont joints dans un cluster (l’ensemble se compose donc de 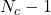 membres). De ce nouveau cluster, le classifieur le plus précis sera sélectionné et ainsi de suite. Le critère d’arrêt sera la meilleure performance possible de l’ensemble, performance qui sera évaluée avec un jeu de données différent de celui utilisé pour l’apprentissage
membres). De ce nouveau cluster, le classifieur le plus précis sera sélectionné et ainsi de suite. Le critère d’arrêt sera la meilleure performance possible de l’ensemble, performance qui sera évaluée avec un jeu de données différent de celui utilisé pour l’apprentissage - En posant
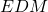 (Ensemble Diversity Measure) comme la proportion d’individus pour lesquels la proportion de votes corrects est située entre 10 et 90 (ces points sont donc considérés comme incertains), il existe un algorithme d’amincissement de l’ensemble. Le but est d’enlever itérativement les classifieurs qui ont le plus souvent tord sur l’ensemble des points incertains. La valeur de la précision du classifieur doit être comprise entre
(Ensemble Diversity Measure) comme la proportion d’individus pour lesquels la proportion de votes corrects est située entre 10 et 90 (ces points sont donc considérés comme incertains), il existe un algorithme d’amincissement de l’ensemble. Le but est d’enlever itérativement les classifieurs qui ont le plus souvent tord sur l’ensemble des points incertains. La valeur de la précision du classifieur doit être comprise entre 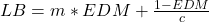 et
et 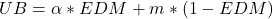 avec
avec 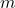 la performance moyenne des classifieurs (ceux présents dans l’ensemble en cours),
la performance moyenne des classifieurs (ceux présents dans l’ensemble en cours),  le nombre de classes et
le nombre de classes et 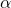 le paramètre de l’algorithme (valeur recommandée : 0.9)
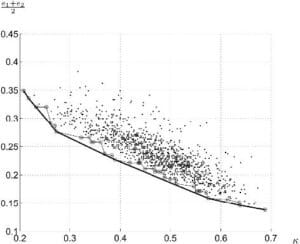
le paramètre de l’algorithme (valeur recommandée : 0.9) - Comme cité plus haut, la répartition des classifieurs selon leur diversité par paire et leur erreur moyenne peut se faire de façon graphique. Ainsi, nous pouvons sélectionner les classifieurs permettant de former l’enveloppe convexe de l’ensemble
- La matrice de diversité portant l’ensemble des valeurs du critère de la double faute est créée, et un nombre donné de classifieurs est choisi parmi les moins représentés. Une sorte de « pruning » analogue peut être réalisé sur la valeur de
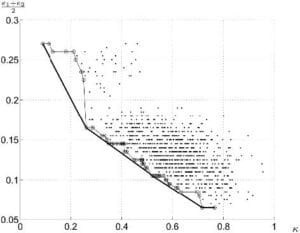
Figure 2.2.4.2 – Kappa-error de 50 classifieurs et son enveloppe convexe -
Toutes ces méthodes ne sont applicables que dans le cas de la combinaison statique de classifieurs ; même si la combinaison peut être construite dynamiquement (en choisissant par exemple les classifieurs apportant la plus grande diversité entre eux) elle passe obligatoirement par la mise en coopération de plusieurs classifieurs. Or, nous nous intéressons à la possibilité de choisir dynamiquement, pour un individu donné, un seul classifieur. Néanmoins, dans le contexte de notre travail, même si ces différentes mesures ne nous permettent pas de répondre au propos d’une combinaison dynamique, elles restent pertinentes pour choisir de façon préalable un jeu de classifieurs, ou pour raffiner ce choix de façon hors-ligne après un certain nombre d’itération du processus de décision. Dans ce cas, comment peut-on mesurer la qualité d’un seul classifieur, sans se référencer à un groupe de classifieur mis en coopération? Nous estimons de plus que le classifieur seul n’est pas tout ; il faut s’intéresser au couple (classifieur, attributs) car la performance du classifieur dépend en partie de la répartition des attributs dans son espace de pavage.
3 SÉLECTION DYNAMIQUE D’UN CLASSIFIEUR
3.1 INTRODUCTION
Dans le cadre de la sélection locale de classifieurs dans l’espace des attributs, les systèmes à classifieurs multiples (MCS) basés sur la combinaison de différents classifieurs sont très utilisés pour atteindre de hautes performances en reconnaissance de formes ou motifs. Dans le principe, pour chaque motif entrant, chaque classifieur calcule sa décision, puis celles ci sont fusionnées à partir de votes majoritaires, approches statistiques, théorie de l’évidence ou fonctions de croyance.
La littérature est essentiellement orientée vers l’idée de combiner a priori différentes décisions de classifieurs à la fin d’un apprentissage plus ou moins élaboré (voir les neuf workshops internationaux sur le problème du « Multiple Classifier Systems »![]() ). Plusieurs études ont été réalisées sur le sujet [5][9][37]. Hand, dans [13], propose de séparer les méthodes en deux classes. La première regroupe les approches combinant les classifieurs sur chacune des entrées ou de leur combinaison [1][24] ou bien sur les sorties des classifieurs [27][33]. La seconde est basée sur une combinaison prenant en compte le contexte en utilisant une combinaison a priori [17][19][28][31] ou une combinaison en cascade [2][15][34]. Mais l’idée de choisir le classifieur dynamiquement en fonction de l’individu requête est encore rare [3].
). Plusieurs études ont été réalisées sur le sujet [5][9][37]. Hand, dans [13], propose de séparer les méthodes en deux classes. La première regroupe les approches combinant les classifieurs sur chacune des entrées ou de leur combinaison [1][24] ou bien sur les sorties des classifieurs [27][33]. La seconde est basée sur une combinaison prenant en compte le contexte en utilisant une combinaison a priori [17][19][28][31] ou une combinaison en cascade [2][15][34]. Mais l’idée de choisir le classifieur dynamiquement en fonction de l’individu requête est encore rare [3].
Selon [70], la première idée de sélection dynamique d’un classifieur est véritablement apparue dans [80], où une description de l’espace des attributs est proposée en utilisant une fonction de dissension entre classifieurs. Intuitivement, les classifieurs tendent à être d’accord sur les cas « faciles » et inversement pour les cas « difficiles ». L’espace est alors partitionné et, pour chaque partie, un modèle de régression est estimé. Dans un second temps, une fonction des décisions des classifieurs est construite dynamiquement, selon la position spatiale des individus à classer. Huang et Suen proposèrent dans [16] une première méthode pour résoudre l’hypothèse d’indépendance à l’erreur inhérente aux combinaisons de classifieurs. Puis, Woods soumet une méthode réelle de sélection dynamique de classifieurs utilisant l’analyse de la précision locale [36] et finalement, Giacinto et al. propose une étude générique pour combiner localement les classifieurs dans l’espace des attributs [12][10].
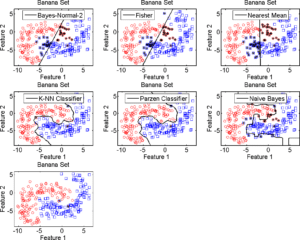
La figure 3.1.1 représente les réponses d’un groupe de classifieur à un jeu de données artificielles (Type « Banana »). Les astérisques indiquent les erreurs d’attribution. Ces exemples montrent le comportement de chaque classifieur en fonction des positions des individus dans l’espace des attributs. Le point intéressant est la différence de forme des frontières pour chaque classifieur; les méthodes linéaires (règle de Bayes, Fisher, plus proche moyenne) séparent le problème en deux solutions simples, tandis que les approches non linéaires apportent une meilleure séparation grâce à une frontière complexe.
Pour les méthodes non linéaires, les individus proches des centres des classes sont les mieux classés, les erreurs étant distribuées le long des frontières. Mais ces erreurs sont différentes selon les classifieurs. La sélection dynamique de classifieurs (DCS) améliore la robustesse du processus de classification pour les individus localisés dans les zones « difficiles » de l’espace des attributs (éloignement du centre des classes, frontières etc.). Ce gain est dû à la diversité des erreurs des classifieurs [19][20][18]; excepté pour les cas où tous les classifieurs se trompent, cela améliore la probabilité de bonne classification pour chaque individu.
3.2 DÉCIDER DYNAMIQUEMENT
Au sein de cette partie, nous étudions les méthodes de combinaison dynamique de classifieurs basées sur la mesure de la précision locale, et l’évaluation de la décision. Voyons en premier lieu le formalisme associé ainsi que son utilisation.
3.2.1 COMBINER LES DÉCISIONS
Soit ![]() un ensemble de
un ensemble de ![]() classifieurs, tous entraînés sur un jeu de
classifieurs, tous entraînés sur un jeu de ![]() classes
classes ![]() . L’ensemble
. L’ensemble ![]() des individus
des individus ![]() est exprimé dans l’espace des attributs
est exprimé dans l’espace des attributs ![]() .
.
Soit ![]() avec
avec ![]() l’ensemble de tous les individus connus (i.e. l’ensemble d’apprentissage) et
l’ensemble de tous les individus connus (i.e. l’ensemble d’apprentissage) et ![]() l’ensemble de tous les individus inconnus (i.e. l’ensemble de test). Chaque sortie de classifieur pour l’individu
l’ensemble de tous les individus inconnus (i.e. l’ensemble de test). Chaque sortie de classifieur pour l’individu ![]() est notée
est notée ![]() .
.
(3.2.1.1) ![]()
Soit ![]() la définition du voisinage de taille
la définition du voisinage de taille ![]() (équation 3.2.1.1).
(équation 3.2.1.1).
Nous définissons la précision locale estimée ![]() pour le classifieur
pour le classifieur ![]() pour un individu
pour un individu ![]() dans le voisinage
dans le voisinage ![]() .
.
Le voisinage considéré est restreint à l’ensemble d’apprentissage ![]() pour lequel chaque classe d’appartenance est définie.
pour lequel chaque classe d’appartenance est définie.
(3.2.1.2) ![]()
La fonction de décision permet alors de déterminer la meilleure décision d’assignation pour l’individu ![]() , pour lequel la classe d’appartenance est inconnue. La décision est prise au sens de la précision locale
, pour lequel la classe d’appartenance est inconnue. La décision est prise au sens de la précision locale ![]() dans le voisinage
dans le voisinage ![]() de taille
de taille ![]() . Cette décision est donnée par le classifieur présentant la plus grande précision dans
. Cette décision est donnée par le classifieur présentant la plus grande précision dans ![]() (algorithme DCS-LA) comme définie par l’équation 3.2.1.3.
(algorithme DCS-LA) comme définie par l’équation 3.2.1.3.
(3.2.1.3) ![]()
3.2.2 PRENDRE EN COMPTE LE VOISINAGE (MCB)
Afin de préciser la notion de voisinage local, Giacinto [11] propose une extension utilisant le concept de comportement de plusieurs classifieurs (multiple classifier behavior ou MCB)[16] pour le calcul des ![]() plus proches voisins.
plus proches voisins.
Le voisinage d’un individu donné ![]() est défini par le vecteur
est défini par le vecteur ![]() dont les éléments sont les décisions de classification pour l’individu
dont les éléments sont les décisions de classification pour l’individu ![]() prises par les
prises par les ![]() classifieurs. Giacinto propose alors une mesure de similarité entre les individus
classifieurs. Giacinto propose alors une mesure de similarité entre les individus ![]() et
et ![]() :
:
(3.2.2.1) 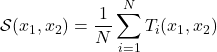
où les fonctions ![]() ,
, ![]() sont définies par :
sont définies par :
(3.2.2.2) ![]()
La fonction ![]() prend valeurs dans
prend valeurs dans ![]() ,
, ![]() si les
si les ![]() décisions de classification sont les mêmes pour
décisions de classification sont les mêmes pour ![]() et
et ![]() , et
, et ![]() si toutes les decisions sont totalement différentes pour les deux individus. Ainsi, Giacinto propose de choisir les
si toutes les decisions sont totalement différentes pour les deux individus. Ainsi, Giacinto propose de choisir les ![]() plus proches voisins de l’individu à classifier, en terme de distance Euclidienne, mais satisfaisant une contrainte de seuil sur la similarité MCB. Dans [11], Giacinto note que, grâce à l’utilisation de l’information du MCB, les performances sont peu affectées par la valeur du paramètre
plus proches voisins de l’individu à classifier, en terme de distance Euclidienne, mais satisfaisant une contrainte de seuil sur la similarité MCB. Dans [11], Giacinto note que, grâce à l’utilisation de l’information du MCB, les performances sont peu affectées par la valeur du paramètre ![]() .
.
3.2.3 MESURER LA PRÉCISION
La qualité de la décision finale dépend de la qualité de l’estimation de la précision locale. Elle est basée sur la capacité d’un classifieur à associer la décision ![]() à la bonne classe
à la bonne classe ![]() pour les individus de l’ensemble d’apprentissage
pour les individus de l’ensemble d’apprentissage ![]() autour de l’individu à classer
autour de l’individu à classer ![]() . Nous supposons alors que le classifieur
. Nous supposons alors que le classifieur ![]() affecte
affecte ![]() à la classe
à la classe ![]() :
: ![]() et proposons différentes mesure de la précision locale pour cette décision.
et proposons différentes mesure de la précision locale pour cette décision.
Soit ![]() , l’ensemble des bonnes réponses dans le
, l’ensemble des bonnes réponses dans le ![]() -voisinage de
-voisinage de ![]() , c’est à dire l’ensemble des individus bien classés dans le voisinage de
, c’est à dire l’ensemble des individus bien classés dans le voisinage de ![]() .
.
(3.2.3.1) ![]()
Trois propositions initiales de la mesure de la précision locale ont été initialement définies [36][10][3] :
- Précision locale a priori
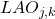 pour le classifieur
pour le classifieur 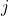 selon un voisinage de
selon un voisinage de 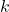 individus :
individus :
(3.2.3.2)
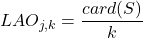
Cette mesure est appelée « a priori » (ou overall LA) car elle ne prend pas en compte la classe attribuée à l’individu
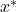 par le classifieur
par le classifieur 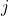 . Elle analyse la capacité du classifieur à prendre la bonne décision pour les classes existantes dans le voisinage de
. Elle analyse la capacité du classifieur à prendre la bonne décision pour les classes existantes dans le voisinage de 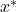 .
. - Précision locale a posteriori (ou local class accuracy)
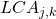 pour le classifieur
pour le classifieur 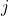 selon un voisinage de
selon un voisinage de 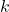 individus :
individus :
(3.2.3.3)
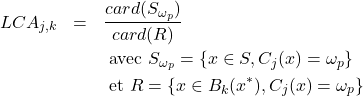
Cette mesure reprend le principe de la méthode classique de mesure de la précision particulièrement utilisée en indexation, et estime le ratio entre le nombre d’individus bien classés dans
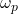 et ceux assignés à cette classe. Elle est alors dédiée à la classe d’affection et limitée par l’hypothèse que la classification ne fasse pas d’erreur affectant la classe
et ceux assignés à cette classe. Elle est alors dédiée à la classe d’affection et limitée par l’hypothèse que la classification ne fasse pas d’erreur affectant la classe 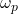 à un individu. D’autre part, cette méthode ne prend pas en compte les individus oubliés appartenant à
à un individu. D’autre part, cette méthode ne prend pas en compte les individus oubliés appartenant à 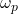 mais non retrouvés (
mais non retrouvés (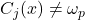 ).
). - Précision locale probabiliste
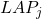 pour le classifieur
pour le classifieur 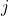 :
:
(3.2.3.4)
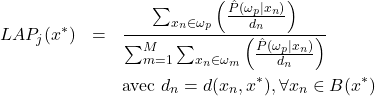
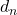 est la distance entre l’individu connu
est la distance entre l’individu connu 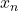 et
et 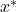 . Didaci n’indique pas le type de distance utilisé (L1, L2, etc.). Nous discuterons plus loin du choix de la métrique de la distance.
. Didaci n’indique pas le type de distance utilisé (L1, L2, etc.). Nous discuterons plus loin du choix de la métrique de la distance.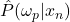 est l’estimation de la probabilité a posteriori d’avoir la classe
est l’estimation de la probabilité a posteriori d’avoir la classe 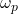 avec les attributs de
avec les attributs de 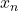 . Une telle formulation exprime un rapport du type densité intra-classe sur la densité inter-classes. L’aspect intra-classes apparaît au numérateur par la capacité des individus de la classe d’affectation à représenter cette classe avec leurs attributs. L’aspect inter-classes est d’autre part lié à l’incapacité des autres classes, dans le voisinage de
. Une telle formulation exprime un rapport du type densité intra-classe sur la densité inter-classes. L’aspect intra-classes apparaît au numérateur par la capacité des individus de la classe d’affectation à représenter cette classe avec leurs attributs. L’aspect inter-classes est d’autre part lié à l’incapacité des autres classes, dans le voisinage de 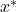 , à représenter la classe
, à représenter la classe 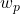 . Pondérer avec la distance
. Pondérer avec la distance 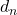 permet de réduire l’impact de cette information par rapport à la distance dans le voisinage d’ordre
permet de réduire l’impact de cette information par rapport à la distance dans le voisinage d’ordre 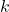 .
.La limite de la proposition de Didaci [] réside dans le fait que le dénominateur de sa formule intègre également l’estimation du numérateur, ce qui déforme le jugement. La raison d’une telle formulation est la nécessité de normaliser la valeur de la précision entre 0 et 1, ce qui fait perdre le pouvoir de discrimination quand deux (ou plus) classes ont presque les mêmes centres.
Toutes ces méthodes donnent une estimation de la précision locale, normalisée entre 0 et 1, ce qui est nécessaire pour les comparer l’une à l’autre. Cependant, la problématique n’est pas de choisir dynamiquement la meilleure méthode de calcul de la précision locale mais le meilleur classifieur selon une métrique de précision choisie a priori. Ainsi, toute comparaison relative des mesures de précision est utilisable. Une fois la contrainte de normalisation rejetée, nous pouvons essayer de définir une nouvelle méthode de mesure de la précision à partir de celles définies précédemment.
Pour le calcul de la précision locale, il est nécessaire de définir les individus connus autour de l’individu inconnu à classer. Didaci définit la précision locale a priori comme étant la moyenne de toutes les précisions locales de tous les classifieurs, sur tous les individus connu du voisinage. L’inconvénient de cette méthode est qu’elle suppose le voisinage sphérique (donc défini par une norme euclidienne). Il semble nécessaire de considérer un individu connu en fonction de sa distance à l’individu inconnu. Comme nous n’avons pas d’information à propos de la forme du voisinage, nous proposons d’utiliser la distance entre l’individu inconnu et chacun des individus connus (toujours dans le voisinage) comme pondération de la précision locale (i.e. ![]() ). De plus, nous ne possédons aucune information à propos de l’espace des attributs, particulièrement à propos de son orthogonalité ou de sa normalité. C’est pourquoi nous nous restreignons à une distance L1 et nous définissons ainsi
). De plus, nous ne possédons aucune information à propos de l’espace des attributs, particulièrement à propos de son orthogonalité ou de sa normalité. C’est pourquoi nous nous restreignons à une distance L1 et nous définissons ainsi ![]() comme :
comme :
(3.2.3.5) ![]()
Dans l’optique de choisir la meilleur fonction de pondération, nous avons d’abord besoin de savoir comment évolue la distance. Nous avons ainsi étudié son évolution pour chaque jeu de données dans la région la plus dense de l’espace de attributs ainsi que dans la plus clairsemée. Les figures 3.2.3.1 et 3.2.3.2 montrent le comportement de la distance (tracé avec l’écart-type), son inverse, log et exponentielle.
Le paramètre ![]() est choisi comme constante de valeur faible pour éviter les opérations non définies (i.e. division par zéro).
est choisi comme constante de valeur faible pour éviter les opérations non définies (i.e. division par zéro).
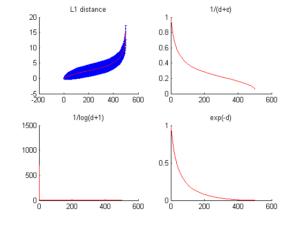
La distance tracée ici est la moyenne de toutes les distances de chaque individu aux autres. Nous présentons aussi dans les tables 3.2.3.1, 3.2.3.2, 3.2.3.3 et 3.2.3.4 l’évolution de la distance dans le voisinage de l’individu moyennement plus proche des autres (l’individu dont la distance moyenne à tous les autres est la plus faible) et celui moyennement le plus éloigné (l’individu dont la distance moyenne à tous les autres est la plus forte).
| 0 | 0.010 | 0.014 | 0.015 | 0.018 | 0.029 | 0.030 | 0.031 | 0.034 | |
|---|---|---|---|---|---|---|---|---|---|
| 1.000 | 0.990 | 0.986 | 0.985 | 0.982 | 0.972 | 0.970 | 0.970 | 0.967 | |
| 969 | 88 | 66 | 61 | 52 | 33 | 32 | 31 | 29 | |
| 1.000 | 0.990 | 0.986 | 0.985 | 0.982 | 0.971 | 0.970 | 0.969 | 0.967 |
![]() 0.2060.5440.0490.0200.0120.0100.0090.0070.005
0.2060.5440.0490.0200.0120.0100.0090.0070.005
| 1.580 | 2.910 | 3.000 | 3.890 | 4.400 | 4.530 | 4.720 | 4.910 | 5.320 | |
|---|---|---|---|---|---|---|---|---|---|
| 0.388 | 0.256 | 0.250 | 0.204 | 0.185 | 0.181 | 0.175 | 0.169 | 0.158 | |
| 1.050 | 0.733 | 0.721 | 0.630 | 0.593 | 0.585 | 0.573 | 0.563 | 0.542 |
| 0.360 | 9.30 | 133 | 162 | 480 | 766 | 1250 | 1250 | 1530 | |
|---|---|---|---|---|---|---|---|---|---|
| 0.027 | 0.010 | 0.007 | 0.006 | 0.002 | 0.001 | 0 | 0 | 0 | |
| 0.277 | 0.220 | 0.204 | 0.196 | 0.162 | 0.151 | 0.140 | 0.140 | 0.136 | |
| 2e-16 | 4e-41 | 1e-58 | 4e-71 | 3e-209 | 0 | 0 | 0 | 0 |
Table 3.2.3.3 – 9 plus proches voisins pour l’individu moyennement le plus lointain – Données Breast Cancer Wisconsin
| 5e6 | 1e7 | 1e7 | 1e7 | 1e7 | 1e7 | 1e7 | 1e7 | 1e7 | |
|---|---|---|---|---|---|---|---|---|---|
| 1e-7 | 8e-8 | 8e-8 | 8e-8 | 8e-8 | 8e-8 | 8e-8 | 8e-8 | 8e-8 | |
| 0.064 | 0.061 | 0.061 | 0.061 | 0.061 | 0.061 | 0.061 | 0.061 | 0.061 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Le jeu de données Breast Cancer Wisconsin présente la plus grande variation de distance entre les individus (tables 3.2.3.3 et 3.2.3.4). Les données du jeu Complex présentent également de fortes variations mais de beaucoup plus petites distances (tables 3.2.3.1 et 3.2.3.2). Avec les résultats associés, nous observons que ![]() est plus discriminant que
est plus discriminant que ![]() qui est limité par son domaine de définition (
qui est limité par son domaine de définition (![]() ). L’expression
). L’expression ![]() atténue également la répartition entre les voisins. Comme il s’agit d’un problème de dynamique de distance, le choix de la méthode de pondération est donc basé sur le gradient
atténue également la répartition entre les voisins. Comme il s’agit d’un problème de dynamique de distance, le choix de la méthode de pondération est donc basé sur le gradient ![]() de
de ![]() . Par exemple, quand
. Par exemple, quand ![]() ,
, ![]() tandis que
tandis que ![]() , nous considérons alors tout le voisinage dans un cas non dans l’autre. C’est pour cela que nous proposons l’usage direct de la distance L1 comme pondération de la précision locale afin d’améliorer les résultats en utilisant une méthode de calcul nécessitant un faible coût de calcul.
, nous considérons alors tout le voisinage dans un cas non dans l’autre. C’est pour cela que nous proposons l’usage direct de la distance L1 comme pondération de la précision locale afin d’améliorer les résultats en utilisant une méthode de calcul nécessitant un faible coût de calcul.
![]() : mesure de la densité des individus correctement classés (
: mesure de la densité des individus correctement classés (![]() ).
).
(3.2.3.6) ![]()
Cette mesure estime le taux d’individus bien classés en prenant en compte la distance à l’individu requête. De la même manière que la précision locale a priori, elle ne prend en compte que la capacité du classifieur à ne pas faire d’erreur sur l’ensemble des classes du voisinage.
4 RÉSULTATS
4.1 LES JEUX DE TEST
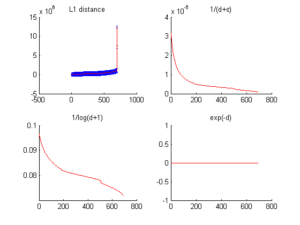
Afin d’étudier le comportement des sélections dynamiques, nous réalisons différents types de tests. Le premier est basé sur un jeu de données artificielles simulant différents types de nuages spécifiques dans un espace d’attributs à deux dimensions. Le second utilise des données réelles sur de plus grandes dimensions. Tous les tests se font sur des problèmes à deux classes, utilisant les données suivantes :
- données artificielles : 4 types de problèmes (Banana, Complex, Difficult et Simple) avec 250 individus par classe, sur 2 dimensions (voir la figure 4.1.1), produites avec un générateur aléatoire
- données naturelles : 5 types de problèmes (base UCI Repository of machine learning databases
 ) décrites dans la table 4.1.1
) décrites dans la table 4.1.1
Nom Taille classe 1 Taille classe 2 Dimension Wisconsin breast cancer 458 241 10 Ionosphere 225 126 34 Pima Indians diabetes 500 268 8 Sonar 97 111 60 German 700 300 24 Table 4.1.1 – Caractéristiques du jeu de données naturelles
4.2 LES CLASSIFIEURS COMBINES
La performance de la combinaison est évaluée à partir des 6 classifieurs suivants :
- QBNC : Classifieur quadratique Bayesien Normal à un noyau par classe(Bayes-Normal-2) ;
- FLSLC : Classifieur linéaire moindres carrées de Fisher ;
- NMC : Classifieur aux plus proches moyennes ;
- KNNC : Classifieur aux
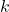 plus proches voisins ;
plus proches voisins ; - ParzenC : Classifieur Parzen ;
- BayesN : Classifieur Bayesien naïf.
Chacun de ces classifieurs a d’abord été entraîné et testé sur tous les jeux de données afin d’en évaluer leurs performances globales. Les jeux d’entraînement et de test ont été construits par bootstrapping[20] à partir des données originales, avec intersection nulle entre les 2 jeux de données à chaque fois.
Le bootstrap est généralement utile à l’estimation de la distribution d’une statistique (moyenne, variance, etc.). Parmi les différentes méthodes citons l’algorithme Monte Carlo [25] permettant un ré-échantillonnage simple. L’idée est de faire une première mesure de la statistique recherchée sur le jeu de données disponible, puis d’échantillonner aléatoirement (avec remise) ce jeu de données et de recommencer la mesure. Cette méthode sera répétée jusqu’à atteindre une précision acceptable.
Les classifieurs KNNC, ParzenC et NMC sont adaptatifs, la valeur de leurs paramètres (i.e. ![]() pour KNNC et ParzenC) est optimisée durant la phase d’apprentissage. Ensuite, une fois le paramètre fixé, il n’est pas remis en cause durant la reconnaissance.
pour KNNC et ParzenC) est optimisée durant la phase d’apprentissage. Ensuite, une fois le paramètre fixé, il n’est pas remis en cause durant la reconnaissance.
4.3 LES MÉTHODES DE COMBINAISON
Nous choisissons de tester les différentes combinaisons selon les différentes façons de calculer la précision locale:
- LAO : précision locale a priori selon [36] (équation 3.2.3.2) ;
- précision locale a posteriori toujours selon [36] (équation 3.2.3.3) ;
- LAP : La méthode de Didaci [3] (équation 3.2.3.4) ;
- LAS : la méthode proposée selon l’équation 3.2.3.6.
Les méthodes LAO, LCA et LAS ont également été comparées en utilisant la contrainte de similarité de Giacinto (approche MCB)[16][11]. Pour ces tests, nous faisons évoluer la taille du voisinage (![]() ) afin de tester son influence sur les résultats. Nous fixons une valeur maximale de
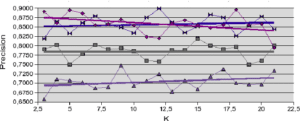
) afin de tester son influence sur les résultats. Nous fixons une valeur maximale de ![]() plus faible que le nombre total d’individus afin de rester dans le cas de l’analyse de la précision locale, et non globale. Pour les résultats présentés ci-dessous, nous utilisons la légende de la figure ??.
plus faible que le nombre total d’individus afin de rester dans le cas de l’analyse de la précision locale, et non globale. Pour les résultats présentés ci-dessous, nous utilisons la légende de la figure ??.
Afin de situer les résultats exprimés en temps de calcul, il faut savoir que tous les tests sont exécutés sur un ordinateur équipé d’un AMD Athlon XP2600+ avec 1Go RAM sous Ubuntu 7.x.
5 DISCUSSION
5.1 LES APPROCHES DIRECTES
L’analyse des comportements sur les jeux de données Banana et Difficult (figures 5.2.1 et 5.2.2) donnent une première idée sur le comportement des mesures de la précision. Pour le jeu Banana, la mesure de précision a posteriori (LCA) est la seule qui augmente en fonction de la taille du voisinage. Dans ce cas de figure, l’accroissement de la taille du voisinage (![]() ) permet l’accroissement du ratio entre le nombre d’individus bien classés et le nombre d’individus reconnus. Pour le jeu de données Difficult (figure 5.2.2), c’est la méthode LAP qui augmente légèrement avec
) permet l’accroissement du ratio entre le nombre d’individus bien classés et le nombre d’individus reconnus. Pour le jeu de données Difficult (figure 5.2.2), c’est la méthode LAP qui augmente légèrement avec ![]() . Ici, l’accroissement de
. Ici, l’accroissement de ![]() est pondéré par la distance à l’individu à reconnaître pour améliorer la mesure de précision. Dans tous les autres cas, la précision est au mieux à peu près stable et au pire décroît légèrement avec l’accroissement de la taille du voisinage.
est pondéré par la distance à l’individu à reconnaître pour améliorer la mesure de précision. Dans tous les autres cas, la précision est au mieux à peu près stable et au pire décroît légèrement avec l’accroissement de la taille du voisinage.
5.2 LES APPROCHES PAR LIMITATION DU VOISINAGE
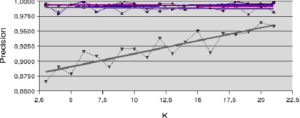
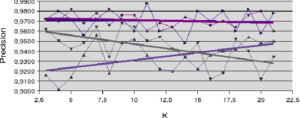
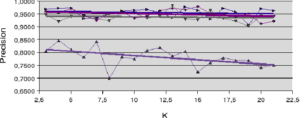
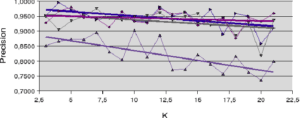
A propos des résultats produits avec les jeux de données artificielles (figures 5.2.1 et 5.2.2) notons la sensible variation de performance pour les méthodes LAO, LCA and LAP (avec ou sans MCB), en comparaisons des résultats obtenus avec les jeux de données naturelles (figures 5.2.3, 5.2.4 et 5.2.5). Les méthodes LAO and LCA prennent en compte le nombre d’individus du voisinage bien classés, mais, lorsque le voisinage grandit, la performance tend vers celle du plus efficace des classifieurs pris seul, ce que nous notons en intégrant les performances des classifieurs seuls (tables 5.3.1 et 5.3.3) dans les figures ci-dessous. Prenons a contrario les données naturelles, dont la densité de distribution est plus faible (les individus sont mieux répartis dans l’espace des attributs), une approche statistique est alors plus représentative du comportement global (et non le meilleur classifieur). Comme les lois de probabilité sont inconnues, nous mesurons la distribution des individus selon 2 critères : la distance moyenne Euclidienne ![]() entre individus, et son écart-type
entre individus, et son écart-type ![]() . Les données sont présentées dans le tableau 5.2.1. Plus la distance moyenne et l’écart-type sont grands, moins la taille du voisinage pour le DCS a d’influence sur la performance globale. Il est également intéressant de noter que la méthode LAS (avec ou sans MCB) semble la moins sensible à la taille du voisinage, excepté bien sûr, le fait que plus
. Les données sont présentées dans le tableau 5.2.1. Plus la distance moyenne et l’écart-type sont grands, moins la taille du voisinage pour le DCS a d’influence sur la performance globale. Il est également intéressant de noter que la méthode LAS (avec ou sans MCB) semble la moins sensible à la taille du voisinage, excepté bien sûr, le fait que plus ![]() est grand, moins bonne est la performance globale (car elle tend vers la performance globale du meilleur classifieur pris seul).
est grand, moins bonne est la performance globale (car elle tend vers la performance globale du meilleur classifieur pris seul).
Notons dans la table 5.2.1 que pour les données artificielles (Banana, Complex, Difficult et Simple) les moyennes et écarts-type sont du même ordre, pour une dimension fixée à 2. Ce qui n’est pas le cas pour les données naturelles, pour lesquelles les rapports entre les distances moyennes et les écarts-type indiquent la très grande complexité de ces bases.
| données | dimension | ||
|---|---|---|---|
| Wisconsin breast cancer | 10 | ||
| Pima Indians diabetes | 8 | ||
| German | 24 | ||
| Ionosphere | 34 | ||
| Sonar | 60 | ||
| Banana set | 2 | ||
| Complex set | 2 | ||
| Difficult set | 2 | ||
| Simple set | 2 |
5.3 L’APPORT DU MULTIPLE CLASSIFIER BEHAVIOR (MCB)
Les ![]() plus proches voisins d’un individu de test sont d’abord identifiés dans le jeux de données d’apprentissage. Ceux caractérisés par des MCB « similaires » (équation 3.2.2.1) à ceux des individus inconnus (issus du jeu de test) sont alors sélectionnés pour calculer les précisions locales et effectuer la sélection dynamique.
plus proches voisins d’un individu de test sont d’abord identifiés dans le jeux de données d’apprentissage. Ceux caractérisés par des MCB « similaires » (équation 3.2.2.1) à ceux des individus inconnus (issus du jeu de test) sont alors sélectionnés pour calculer les précisions locales et effectuer la sélection dynamique.
Les tables 5.3.1 et 5.3.3 représentent la meilleure performance pour chaque classifieur seul, puis pour chaque méthode de DCS (pour tous ![]() ). Notons en premier lieu (5.3.3), le gain de performance qu’apporte le MCB aux méthodes LAO et LCA. Ces résultats correspondent aux remarques de Huang formulées dans [16]. En seconde constatation, les résultats de la méthode LAS sont dégradés lors d’une combinaison avec l’approche MCB. En effet, la méthode LAS, basée sur un calcul moyen, nécessite un maximum d’informations à propos du voisinage, or le MCB ne prend pas en compte les individus les plus proches en terme de distance, mais seuls ceux en terme de réponse de classifieur. Ainsi, pour chaque méthode de calcul de la précision globale, le MCB améliore la probabilité de prendre les individus pour lesquels le système présente une meilleure certitude (qui peut s’apparenter à une mesure de crédibilité en théorie de l’évidence), sauf pour notre approche qui n’en a pas besoin. Ainsi, le MCB améliore les performances en sélectionnant l’information selon la similarité des sorties des classifieurs. Cependant, il y a une exception pour les méthodes prenant en compte les distances entre les individus connus et l’individu requête
). Notons en premier lieu (5.3.3), le gain de performance qu’apporte le MCB aux méthodes LAO et LCA. Ces résultats correspondent aux remarques de Huang formulées dans [16]. En seconde constatation, les résultats de la méthode LAS sont dégradés lors d’une combinaison avec l’approche MCB. En effet, la méthode LAS, basée sur un calcul moyen, nécessite un maximum d’informations à propos du voisinage, or le MCB ne prend pas en compte les individus les plus proches en terme de distance, mais seuls ceux en terme de réponse de classifieur. Ainsi, pour chaque méthode de calcul de la précision globale, le MCB améliore la probabilité de prendre les individus pour lesquels le système présente une meilleure certitude (qui peut s’apparenter à une mesure de crédibilité en théorie de l’évidence), sauf pour notre approche qui n’en a pas besoin. Ainsi, le MCB améliore les performances en sélectionnant l’information selon la similarité des sorties des classifieurs. Cependant, il y a une exception pour les méthodes prenant en compte les distances entre les individus connus et l’individu requête ![]() .
.
Nous avons également étudié le comportement d’un groupe de classifieurs construit a priori par optimisation de la diversité. La mesure utilisée est celle de l’entropie, et nous avons sélectionné, pour chaque jeu de données, l’association de classifieurs présentant l’entropie la plus forte. Le taux de bonne classification obtenu est présenté en table 5.3.2.
Nous observons ici que la méthode de construction d’un jeu de classifieur basée sur la diversité n’améliore pas les résultats globaux obtenus par les classifieurs seuls. Ce qui nous laisse à penser que cette méthode n’est pas adaptée pour de la construction dynamique d’ensemble de classifieurs, comparé à une construction statique a priori.
| Banana | Complex | Difficult | Simple | Diabetes | Sonar | German | Cancer | Ionosphere | |
|---|---|---|---|---|---|---|---|---|---|
| Quadratic | 0.87 | 0.83 | 0.96 | 0.86 | 0.71 | 0.81 | 0.74 | 0.96 | 0.92 |
| Pseudo Fisher | 0.87 | 0.47 | 0.96 | 0.86 | 0.72 | 0.84 | 0.69 | 0.95 | 0.85 |
| Nearest Mean | 0.82 | 0.47 | 0.72 | 0.86 | 0.59 | 0.70 | 0.58 | 0.52 | 0.76 |
| KNN | 0.99 | 0.93 | 0.97 | 0.93 | 0.86 | 0.92 | 0.86 | 0.84 | 0.94 |
| Parzen | 0.99 | 0.88 | 0.95 | 0.89 | 0.74 | 0.92 | 0.63 | 0.51 | 0.92 |
| Naive Bayesian | 0.94 | 0.80 | 0.69 | 0.85 | 0.74 | 0.88 | 0.68 | 0.98 | 0.50 |
| Best Performance | 0.99 | 0.93 | 0.97 | 0.93 | 0.86 | 0.92 | 0.86 | 0.98 | 0.94 |
| Banana | Complex | Difficult | Simple | Diabetes | Sonar | German | Cancer | Ionosphere | |
|---|---|---|---|---|---|---|---|---|---|
| Mesure de l’entropie | 0.99 | 0.58 | 0.91 | 0.87 | 0.76 | 0.80 | 0.74 | 0.67 | 0.90 |
| Banana | Complex | Difficult | Simple | Diabetes | Sonar | German | Cancer | Ionosphere | |
|---|---|---|---|---|---|---|---|---|---|
| LAO | 1.00 | 0.93 | 0.98 | 0.95 | 0.90 | 0.98 | 0.89 | 0.98 | 0.98 |
| LAO+MCB | 1.00 | 0.94 | 0.98 | 0.95 | 0.90 | 0.99 | 0.90 | 0.99 | 0.99 |
| LCA | 0.96 | 0.91 | 0.97 | 0.91 | 0.82 | 0.97 | 0.85 | 0.97 | 0.98 |
| LCA+MCB | 1.00 | 0.95 | 0.98 | 0.96 | 0.89 | 1.00 | 0.89 | 0.99 | 0.99 |
| LAP | 0.99 | 0.86 | 0.97 | 0.87 | 0.75 | 0.90 | 0.65 | 0.65 | 0.85 |
| LAS | 1.00 | 0.95 | 0.99 | 0.95 | 0.90 | 0.99 | 0.92 | 0.99 | 0.98 |
| LAS+MCB | 0.94 | 0.90 | 0.98 | 0.93 | 0.83 | 0.96 | 0.85 | 0.99 | 0.99 |
| Best Performance | 1.00 | 0.95 | 0.99 | 0.96 | 0.90 | 1.00 | 0.92 | 0.99 | 0.99 |
5.4 L’INTÉRÊT DE LA COMBINAISON DYNAMIQUE
Les résultats obtenus par combinaison statique a priori de classifieurs par optimisation de la diversité sont très faibles, comparés aux classifieurs seuls ou combinés dynamiquement, pour les données « Complex » ou « Breast Cancer Wisconsin ». Ce comportement peut s’expliquer par le fait que la diversité est un critère basé sur le comportement global qui compare un classifieur par rapport au groupe, tandis que la précision locale est un critère basé sur la répartition des individus dans l’espace des attributs.
Notons finalement que pour les jeux de données testés, les résultats donnés par DCS sont toujours meilleurs que ceux obtenus par le meilleur classifieur pris seul (tables 5.3.1 et 5.3.3).
Les méthodes LCA+MCB et LAS donnent même le meilleur taux de reconnaissance global (table 5.3.3) pour un temps de calcul similaire (environ 80ms par individu pour les données artificielles sur un AMD Athlon XP2600+ avec 1Go RAM sous Ubuntu 7.x). Les bénéfices attendus de la sélection dynamique de classifieurs sont pour les très grosses bases de données, il est alors possible de n’implémenter que quelques classifieurs, certainement pas les meilleurs en terme de performance, mais au moins les meilleurs en terme de temps de calcul. Ainsi, le temps de calcul est grandement amélioré par rapport à un unique classifieur trop complexe. Ceci est particulièrement intéressant face à l’augmentation des techniques d’extraction de la connaissance, data mining [6], où une réponse de plus en plus rapide est attendue alors qu’il faut gérer des quantités de données de plus en plus grandes.
Néanmoins, pour être complet, il faut prendre en compte le coût le plus important de la méthode qui est liée à une recherche de voisinage sur l’ensemble d’apprentissage. Une implémentation pratique de la méthode verrait ici un très grand gain à utiliser des approches optimisées et une organisation de l’ensemble d’apprentissage sous forme d’arbre par exemple.
6 CONCLUSION
Deux idées ont été présentées ici. La première est la mesure de la précision locale pour la classification. La seconde est l’utilisation de cette précision locale dans les systèmes de classifieurs dynamiques (DCS). Nous avons montré l’amélioration apportée par ces idées, comparée à l’utilisation a priori d’un seul classifieur. Nous avons également expliqué l’importance d’utiliser, pour le calcul de la précision locale d’un classifieur, un voisinage de faible taille (la précision locale tendant vers la précision globale lorsque la taille du voisinage augmente). Nous avons finalement proposé une façon différente de calculer la précision locale qui donne des résultats aussi bons que ceux donnés par la meilleure des méthodes existantes mais avec une plus faible complexité algorithmique.
Il est possible de développer d’autres méthodes de mesure de la précision locale en utilisant la connaissance sur les classifieurs, spécialement en utilisant la position des individus inconnus par rapport aux frontières et aux centres des classes. Cette adaptation à la configuration est proche de celle du principe des machines à support vectoriel (SVM) [30].
Cependant, sur ce genre d’approche, quelques précautions sont à prendre en compte avec les contraintes imposées par les données naturelles (i.e. des zéros sur les matrices de variance/covariance).
Nous montrons ici l’intérêt d’utiliser l’information sur la répartition des individus dans l’espace des attributs, spécialement dans un voisinage donné, en utilisant une distance L1 pour le calcul de la précision locale. La suite de ce travail pourra être d’exploiter la forme du voisinage, en utilisant l’information portée par la covariance entre individus (matrices de variance/covariance, valeurs propres), dans l’idée de créer une métrique adaptative comme montré dans [14]. Ce genre de métrique réduit le voisinage dans les directions le long desquelles les centres des classes diffèrent, avec l’intention de finir sur un voisinage pour lequel les centres des classes coïncident (et avoir ainsi le plus proche voisinage approprié pour la classification).
Néanmoins, la mesure de la précision est le point le plus intéressant pour une chaîne de traitement de l’information [7][6]. Avec la capacité d’évaluer la qualité de la décision, le système possède l’information à réinjecter pour l’exécution dynamique des opérateurs et la prise de décision [32].
Si nous revenons au problème de l’intégration de la précision pour la prise de décision, nous venons de voir comment calculer cette précision pour les classifieurs, et comment l’utiliser pour choisir dynamiquement un classifieur, a priori le mieux adapté pour traiter l’individu inconnu en cours d’analyse.
RÉFÉRENCES
[1] C. Conversano, R. Siciliano, and F. Mola. Supervised classifier combination through generalized additive multi-model. In MCS ’00 : Proceedings of the First InternationalWorkshop on Multiple Classifier Systems, pages 167–176, London, UK, 2000. Springer-Verlag.
[2] L. P. Cordella, P. Foggia, C. Sansone, F. Tortorella, and M. Vento. A cascaded multiple expert system for verification. In MCS ’00 : Proceedings of the First International Workshop on Multiple Classifier Systems, pages 330–339, London, UK, 2000. Springer-Verlag.
[3] L. Didaci, G. Giacinto, F. Roli, and G. L. Marcialis. A study on the performances of dynamic classifier selection based on local accuracy estimation. Pattern Recognition, 38 :2188–2191, 2005.
[4] T. G. Dietterich. Approximate statistical tests for comparing supervised classification learning algorithms. Neural Computation, 7(10) :1895–1942, 1998.
[5] R. P.W. Duin and D. M. J. Tax. Experiments with classifier combining rules. In MCS ’00 : Proceedings of the First International Workshop on Multiple Classifier Systems, pages 16–29, London, UK, 2000. Springer-Verlag.
[6] U. Fayyad, G. Pietetsky-Shapiro, and P. Smyth. From data mining to knowledge discovery in databases. AI Magazine, 17(3) :37–54, 1996.
[7] U. Fayyad, G. Pietetsky-Shapiro, and P. Smyth. Knowledge discovery and data mining : towards a unifying framework. Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining, pages 82–88, 1996.
[8] J. L. Fleiss. Statistical Methods for Rates and Proportions. John Wiley & Sons, 1981.
[9] J. Ghosh. Multiclassifier systems : Back to the future. In MCS ’02 : Proceedings of the Third International Workshop on Multiple Classifier Systems, pages 1–15, London, UK, 2002. Springer-Verlag.
[10] G. Giacinto and F. Roli. Adaptive selection of image classifiers. ICIAP ’97, Lecture Notes in Computer Science, 1310 :38–45, 1997.
[11] G. Giacinto and F. Roli. Dynamic classifier selection based on multiple classifier behaviour. Pattern Recognition, 34 :1879–1881, 2001.
[12] G. Giacinto, F. Roli, and G. Fumera. Selection of image classifiers. Electronics Letters, 36(5) :420–422, 2000.
[13] D. J. Hand, N. M. Adams, and M. G. Kelly. Multiple classifier systems based on interpretable linear classifiers. In MCS ’01 : Proceedings of the Second International Workshop on Multiple Classifier Systems, pages 136–147, London, UK, 2001. Springer-Verlag.
[14] T. Hastie and R. Tibshirani. Discriminant adaptive nearest neighbor classification. IEEE Transaction on Pattern Analysis and Machine Intelligence, 18(6) :607–616, 1996.
[15] T. K. Ho. Complexity of classification problems and comparative advantages of combined classifiers. In MCS ’00 : Proceedings of the First International Workshop on Multiple Classifier Systems, pages 97–106, London, UK, 2000. Springer-Verlag.
[16] Y. S. Huang and C. Y. Suen. A method of combining multiple experts for the recognition of unconstrained handwritten numerals. IEEE Trans. on Pattern Analysis and Machine Intelligence, 17 :90–94, 1995.
[17] K. G. Ianakiev and V. Govindaraju. Architecture for classifier combination using entropy measures. In MCS ’00 : Proceedings of the First International Workshop on Multiple Classifier Systems, pages 340–350, London, UK, 2000. Springer-Verlag.
[18] L. I. Kuncheva. Switching between selection and fusion in combining classifiers : an experiment. IEEE Trans. Syst. Man. Cybernet. Part B 32, 2002.
[19] L. I. Kuncheva. Combining Pattern Classifiers. Wiley, 2004.
[20] L. I. Kuncheva, M. Skurichina, and R.P.W. Duin. An experimental study on diversity for bagging and boosting with linear classifiers. Information fusion, pages 245–258, 2002.
[21] P. Latinne, O. Debeir, and C. Decaestecker. Different ways of weakening decision trees and their impact on classification accuracy of dt combination. In MCS ’00 : Proceedings of the First International Workshop on Multiple Classifier Systems, pages 200–209, London, UK, 2000. Springer-Verlag.
[22] L. Lebart, A. Morineau, and M. Piron. Statistique exploratoire multidimensionnelle. DUNOD, 1995.
[23] S.W. Looney. A statistical technique for comparing the accuracies of several classifiers. Pattern Recognition Letters, 8(1) :5–9, 19988.
[24] S. P. Luttrell. A self-organising approach to multiple classifier fusion. In MCS ’01 : Proceedings of the Second International Workshop on Multiple Classifier Systems, pages 319–328, London, UK, 2001. Springer-Verlag.
[25] N. Metropolis. The beginning of the monte carlo method. Los Alamos Science, 15 :125–130, 1987.
[26] J. Parker. Rank and response combination from confusion matrix data. Information Fusion, 2 :113–120, 2001.
[27] F. Roli, G. Fumera, and J. Kittler. Fixed and trained combiners for fusion of imbalanced pattern classifiers. 5th International Conference on Information Fusion, pages 278–284, 2002.
[28] F. Roli, G. Giacinto, and G. Vernazza. Methods for designing multiple classifier systems. In MCS ’01 : Proceedings of the Second International Workshop on Multiple Classifier Systems, pages 78–87, London, UK, 2001. Springer-Verlag.
[29] J. W. Jr Sammon. A nonlinear mapping for data structure analysis. IEEE Transactions on Computers, 18 :401–409, 1969.
[30] J. Shawe-Taylor and N. Cristianini. Support Vector Machines and other kernel-based learning methods. Cambridge University Press, 2000.
[31] M. Skurichina, L. I. Kuncheva, and R. P.W. Duin. Bagging and boosting for the nearest mean classifier : Effects of sample size on diversity and accuracy. In MCS ’02 : Proceedings of the Third International Workshop on Multiple Classifier Systems, pages 62–71, London, UK, 2002. Springer-Verlag.
[32] S. Sochacki, N. Richard, and P. Bouyer. A comparative study of different statistical moments using an accuracy criterion. In Seventh IAPR International Workshop on Graphics Recognition – GREC 2007, September 2007.
[33] D. M. J. Tax and R. P. W. Duin. Combining one-class classifiers. In MCS ’01 : Proceedings of the Second International Workshop on Multiple Classifier Systems, pages 299–308, London, UK, 2001. Springer-Verlag.
[34] P. Viola and M. Jones. Rapid object detection using a boosted cascade of simple features. In IEEE Conference on Computer Vision and Pattern Recognition (CVPR01), volume 1, pages 511–518, Kaui(Hawaii), Décembre 2001.
[35] M. S. Wong and W. Y. Yan. Investigation of diversity and accuracy in ensemble of classifiers using bayesian decision rules. In International Workshop on Earth Observation and Remote Sensing Applications (EORSA 2008), pages 1–6, 2008.
[36] K. Woods, W. P. Kegelmeyer, and K. Bowyer. Combination of multiple classifiers using local accuracy estimates. IEEE Trans. on Pattern Analysis and Machine Intelligence, 19 :405–410, 1997.
[37] L. Xu and A. Krzyzakand C. Y. Suen. Methods for combining multiple classifiers and their applications to handwriting recognition. IEEE Transactions on Systems, Man and Cybernetics, 22(3) :418–435, 1992.
[38] H. Khoufi Zouari. Contribution à l’évaluation des méthodes de combinaison parallèle de classifieurs par simulation. PhD thesis, Université de Rouen, December 2004.
